Inéquation avec des ln
14 messages
- Page 1 sur 1
Inéquation avec des ln
Bonjour à tous,
Je suis bloqué par cette inéquation: ln(x²)<ln(6)
Après calculs j'arrive à: ln(x)<ln(V6), est-ce que c'est correct jusque là?
Merci de me répondre Cordialement lefouineur
Je suis bloqué par cette inéquation: ln(x²)<ln(6)
Après calculs j'arrive à: ln(x)<ln(V6), est-ce que c'est correct jusque là?
Merci de me répondre Cordialement lefouineur
Re: Inéquation avec des ln
Bonjour
Tu as une inéquation comportant le mot log
Où sont tes conditions ?
Revois déjà çà
Ce que tu as écrit n'est pas équivalent à ce que tu as dans ton énoncé...tu devrais justifier chaque passage de ligne pour vérifier que tu utilises bien un résultat autorisé
Tu as une inéquation comportant le mot log
Où sont tes conditions ?
Revois déjà çà
Ce que tu as écrit n'est pas équivalent à ce que tu as dans ton énoncé...tu devrais justifier chaque passage de ligne pour vérifier que tu utilises bien un résultat autorisé
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Inéquation avec des ln
Bonjour vam et merci pour ta réponse,
Je reprends: ln(x²)<ln(6) il faut x²>0 et x>0 or x² est toujours >=0 donc x doit être différent de 0
il faut x>0
condition résultante: x>=0 il vient: 2*ln(x)<ln(6) <=>(2*ln(x))/2<(ln(6))/2 <=> ln(x)<1/2*ln(6) <=> ln(x)<ln(V6)
cette dernière condition peut être remplie: la solution est l'intervalle de zéro exclu à racine de 6 exclu
vam, cela fait un an et demi que je n'ai pas fait de maths, normal que j'ai perdu certains automatismes...
Je reprends: ln(x²)<ln(6) il faut x²>0 et x>0 or x² est toujours >=0 donc x doit être différent de 0
il faut x>0
condition résultante: x>=0 il vient: 2*ln(x)<ln(6) <=>(2*ln(x))/2<(ln(6))/2 <=> ln(x)<1/2*ln(6) <=> ln(x)<ln(V6)
cette dernière condition peut être remplie: la solution est l'intervalle de zéro exclu à racine de 6 exclu
vam, cela fait un an et demi que je n'ai pas fait de maths, normal que j'ai perdu certains automatismes...
Re: Inéquation avec des ln
Je ne comprends pas ta condition
Tu dois avoir je suis d'accord
je suis d'accord
Qu'est ce que cela donne ça ?
Tu dois avoir
Qu'est ce que cela donne ça ?
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Inéquation avec des ln
Bonjour
Une propriété très utile pour les inéquations avec ln, c'est que ln est strictement croissante sur ]0;+inf[
cela signifie que:

Une propriété très utile pour les inéquations avec ln, c'est que ln est strictement croissante sur ]0;+inf[
cela signifie que:
Re: Inéquation avec des ln
catamat, même pour l'ensemble de définition, tu peux prendre la main quand lefouineur repassera...je fais tellement d'autres choses !
merci
merci
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Inéquation avec des ln
Ok Vam, pas de soucis
Pour le Df ce qui n'allait pas cétait
Ok pour x²>0 mais pas pour x>0
Pour le Df ce qui n'allait pas cétait
il faut x²>0 et x>0
Ok pour x²>0 mais pas pour x>0
Re: Inéquation avec des ln
Bonjour à Tous,
Permettez-moi d'intervenir, pour donner ma proposition.
On a :
ln(x²)<ln(6) avec la condition de x²>0 et x différent de 0.
Ce qui implique
ln(x²)-ln(6)<0
Donc ln(x²/6)<ln(1)
x²/6<1 ce qui implique que x²-6<0
(x+V6)(x-V6)<0
Donc les solutions sont :
x(appartient) à )-V6, 0( U)0, +V6(
Merci à tous les intervenants
Permettez-moi d'intervenir, pour donner ma proposition.
On a :
ln(x²)<ln(6) avec la condition de x²>0 et x différent de 0.
Ce qui implique
ln(x²)-ln(6)<0
Donc ln(x²/6)<ln(1)
x²/6<1 ce qui implique que x²-6<0
(x+V6)(x-V6)<0
Donc les solutions sont :
x(appartient) à )-V6, 0( U)0, +V6(
Merci à tous les intervenants
Re: Inéquation avec des ln
Bonjour vam et catamat,
Je vous ai posté un message hier mais celui-ci s'est perdu...
J'avais posé la condition x²>0 mais aussi x>0 avec laquelle vous n'êtes pas d'accord, je vais vous expliquer pourquoi: l'inéquation initiale est: ln(x²)<ln(x)
Regardons le premier membre: l'inéquation est définie si et seulement si x²>0 je suis d'accord...
Regardons maintenant le second membre: cette fois l'inéquation est définie si et seulement si x>0, non?
J'attends vos commentaires, merci d'avance
Cordialement lefouineur
Je vous ai posté un message hier mais celui-ci s'est perdu...
J'avais posé la condition x²>0 mais aussi x>0 avec laquelle vous n'êtes pas d'accord, je vais vous expliquer pourquoi: l'inéquation initiale est: ln(x²)<ln(x)
Regardons le premier membre: l'inéquation est définie si et seulement si x²>0 je suis d'accord...
Regardons maintenant le second membre: cette fois l'inéquation est définie si et seulement si x>0, non?
J'attends vos commentaires, merci d'avance
Cordialement lefouineur
Re: Inéquation avec des ln
Alors là si tu nous dis tout en 36 fois ! 
pour cette "initiale" oui tu arrives bien à x > 0
mais je ne vois pas comment de cette initiale tu arrives à des ln(6) !
peut-on avoir un énoncé depuis le début au mot près stp ?
pour cette "initiale" oui tu arrives bien à x > 0
mais je ne vois pas comment de cette initiale tu arrives à des ln(6) !
peut-on avoir un énoncé depuis le début au mot près stp ?
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Inéquation avec des ln
Oui en effet cela change les données là...
Une remarque en attendant l'énoncé intégral :
Quand on utilise ln x² = 2 lnx on ne peut le faire que dans le cas où x est strictement positif
Or ici on a juste x non nul donc on ne doit pas utiliser ce résultat
Une astuce serait de remplacer x² par |x|² (ils sont égaux)
On a alors ln x² = ln |x|²=2 ln|x| , c'est correct car on a bien |x|>0
Une remarque en attendant l'énoncé intégral :
Quand on utilise ln x² = 2 lnx on ne peut le faire que dans le cas où x est strictement positif
Or ici on a juste x non nul donc on ne doit pas utiliser ce résultat
Une astuce serait de remplacer x² par |x|² (ils sont égaux)
On a alors ln x² = ln |x|²=2 ln|x| , c'est correct car on a bien |x|>0
Re: Inéquation avec des ln
Désolé les amis, je me suis encore planté!
L'énoncé complet est: -Résoudre les inéquations suivantes:
a) ln(x²)<ln(6)
b)exp(3x)-exp(4x)=>0
Voila tout est en ordre maintenant
L'énoncé complet est: -Résoudre les inéquations suivantes:
a) ln(x²)<ln(6)
b)exp(3x)-exp(4x)=>0
Voila tout est en ordre maintenant
Re: Inéquation avec des ln
Bon cela confirme ce que l'on disait
La seule condition d'existence est x²>0 ce qui est équivalent à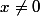
Ensuite le plus simple est d'utiliser la croissance stricte de ln sur ]0;+inf[ ( j'ai rappelé la propriété plus haut...)
L'inéquation est donc équivalente à x²<6 ou x²-6<0, un tableau de signes, permet de conclure... ne pas oublier bien sûr que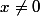
La seule condition d'existence est x²>0 ce qui est équivalent à
Ensuite le plus simple est d'utiliser la croissance stricte de ln sur ]0;+inf[ ( j'ai rappelé la propriété plus haut...)
L'inéquation est donc équivalente à x²<6 ou x²-6<0, un tableau de signes, permet de conclure... ne pas oublier bien sûr que
Re: Inéquation avec des ln
Merci beaucoup pour ta réponse catamat et mes excuses pour ma confusion d'hier. Je pense y arriver tout seul maintenant.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
