23 résultats trouvés
Revenir à la recherche avancée
Oui bien sur, mais si je passe à l'exponentielle d'un côté de l'inégalité, je passe aussi à l'exponentielle de l'autre coté. Et j'aurai le même pb mais avec l'exponentielle au lieu du logarithme, non ??
- 20 Nov 2011, 13:17
- Forum: ✯✎ Supérieur
- Sujet: Inégalité à démontrer
- Réponses: 6
- Vues: 550
Noter que la période constitue les trois derniers chiffres, soit 101
En sommant jusqu'à
- 20 Nov 2011, 13:15
- Forum: ✯✎ Supérieur
- Sujet: Conversion en décimal de nombres binaires
- Réponses: 11
- Vues: 1668
Je ne vois pas comment ça m'aide. En fait j'arrive pas à voir comment je peux "transformer" le 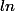 pour n'avoir que des
pour n'avoir que des 
- 20 Nov 2011, 12:54
- Forum: ✯✎ Supérieur
- Sujet: Inégalité à démontrer
- Réponses: 6
- Vues: 550
Le chiffre des unités correspond à 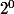
Celui des dizaines à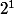
Celui des centaines à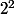
Par exemple 101 = 1*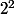 +0*
+0*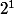 +1*
+1*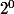
Donc tu fais pareil avec les chiffres après la virgule,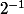 ,
, 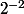 ...
...
Celui des dizaines à
Celui des centaines à
Par exemple 101 = 1*
Donc tu fais pareil avec les chiffres après la virgule,
- 20 Nov 2011, 12:47
- Forum: ✯✎ Supérieur
- Sujet: Conversion en décimal de nombres binaires
- Réponses: 11
- Vues: 1668
Inégalité à démontrer
Bonjour,
comment montrer que :
^{\frac1n}\leq(\frac1n)(x_1+...+x_n))
Dans le début de l'exercice on me demande de majorer)
Je trouve que\leq(x-1)) mais je ne vois pas comment m'en servir.
mais je ne vois pas comment m'en servir.
Une idée pour démarrer?
Merci!
comment montrer que :
Dans le début de l'exercice on me demande de majorer
Je trouve que
Une idée pour démarrer?
Merci!
- 19 Nov 2011, 14:40
- Forum: ✯✎ Supérieur
- Sujet: Inégalité à démontrer
- Réponses: 6
- Vues: 550
géométrie dans l'espace
Bonjour,
Que représente l'ensemble des points A tels que. \vec{AD})
Est-ce que c'est la distance du point D au plan ABC?
Merci
Que représente l'ensemble des points A tels que
Est-ce que c'est la distance du point D au plan ABC?
Merci
- 18 Nov 2011, 15:06
- Forum: ✯✎ Supérieur
- Sujet: géométrie dans l'espace
- Réponses: 2
- Vues: 544
- 17 Nov 2011, 10:57
- Forum: ✯✎ Supérieur
- Sujet: Diagonalisation
- Réponses: 5
- Vues: 667
Voilà sur quoi je suis partie, mais je ne suis pas sure que ce soit la bonne méthode à suivre... u+v+w=1 e^{ix}+e^{iy}+e^{iz}=1 cos(x)+isin(x)+cos(y)+isin(y)+cos(z)+isin(z)=1 d'où cos(x)+cos(y)+cos(z)=1 et sin(x)+sin(...
- 17 Nov 2011, 10:18
- Forum: ✯✎ Supérieur
- Sujet: Ensembles de complexes
- Réponses: 9
- Vues: 1105
- 16 Nov 2011, 17:39
- Forum: ✯✎ Supérieur
- Sujet: Diagonalisation
- Réponses: 5
- Vues: 667
- 16 Nov 2011, 17:35
- Forum: ✯✎ Supérieur
- Sujet: matrices
- Réponses: 2
- Vues: 551
Diagonalisation
Bonjour, je ne comprend pas très bien comment diagonaliser une matrice M de taille nxn En premier, on regarde le polynome caractéristique det(M-X.In) avec In la matrice identité. Si le polynome a des racines dans R alors la matrice est diagonalisable (est-ce qu'il faut que le polynome ait n racines ...
- 16 Nov 2011, 11:47
- Forum: ✯✎ Supérieur
- Sujet: Diagonalisation
- Réponses: 5
- Vues: 667
- 15 Nov 2011, 12:54
- Forum: ✯✎ Supérieur
- Sujet: TI voyage 200
- Réponses: 1
- Vues: 803
- 13 Nov 2011, 18:50
- Forum: ✯✎ Supérieur
- Sujet: Transformation visage
- Réponses: 2
- Vues: 524
Transformation visage
Bonjour,
pouvez vous me dire ce que sont les transformations du plan ou de l'espace appelées "visage" ?
Je ne trouve rien dessus...
Merci pour votre aide
pouvez vous me dire ce que sont les transformations du plan ou de l'espace appelées "visage" ?
Je ne trouve rien dessus...
Merci pour votre aide
- 13 Nov 2011, 17:28
- Forum: ✯✎ Supérieur
- Sujet: Transformation visage
- Réponses: 2
- Vues: 524
Ah oui en effet... :mur: et c'est pas faute d'avoir cherché!!
Je prépare le concours d'inspecteur des finances publiques qui est dans...10jours pile poil!
Je prépare le concours d'inspecteur des finances publiques qui est dans...10jours pile poil!
- 12 Nov 2011, 18:55
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 6
- Vues: 643
v_{n+1}=v_n + \frac1{n(n+1)} = 2-\frac1n + \frac1{n(n+1)} = 2-\frac{n+2}{n(n+1)} En fait il faut que je décompose \frac1{n(n+1)} en éléments simples, ce qui me donne \frac1n - \frac 1{n+1} et du coup j'obtiens bien v_{n+1}=2-\frac1{n+1} . Mais je ne comprends pas pou...
- 12 Nov 2011, 18:21
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 6
- Vues: 643
Soit P_n la propriété suivante : v_n=2-\frac1n Initialisation : v_1=2-1=1 donc P_0 est vraie. Hypothèse de récurrence: P_n est vraie pour un certain n. Montrons que P_{n+1} est toujours vraie au rang n+1. v_{n+1}=v_n + \frac1{n(n+1)} = 2-\frac1n + \frac1{n(n+1)} = 2-\frac{n+2}{n(...
- 12 Nov 2011, 17:17
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 6
- Vues: 643
Suites
Bonjour, je m'entraine pour un concours et j'essaie de résoudre cet exo, mais je bloque... u_1=v_1=1 u_n_+_1=u_n+\frac1{(n+1)^2} v_n_+_1=v_n+\frac1{n(n+1)} 1) Montrer que l'on a v_n=2-\frac1n pour tout n appartenant à N* 2) Montrer que l'on a u_n \leq v_n pour tout n appartenant à N*...
- 12 Nov 2011, 16:19
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 6
- Vues: 643
tan ;) = 4/3
arctan 4/3 = ;) = angle en radian
or: angle en degré = 180 * (angle en radian) / pi
donc: angle en degré = 53,13 degré
arctan 4/3 = ;) = angle en radian
or: angle en degré = 180 * (angle en radian) / pi
donc: angle en degré = 53,13 degré
- 01 Nov 2011, 17:38
- Forum: ✯✎ Supérieur
- Sujet: méthode pour transformer en degré?
- Réponses: 4
- Vues: 647
Suite récurrente linéaire
Bonjour, quelqu'un peut m'aider à résoudre cette exercice? Je ne comprends pas la solution... Je mets le lien de l'exercice, c'est plus lisible. C'est l'exercice 1: http://mp.cpgedupuydelome.fr/mesexos.php?idSect=367 Je résous l'équation caractéristique équivalente à coefficients complexes et je tro...
- 01 Nov 2011, 16:43
- Forum: ✯✎ Supérieur
- Sujet: Suite récurrente linéaire
- Réponses: 0
- Vues: 367
- 23 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
