Oki, merci bien, j'y ai fait un tour et je pense que cela m'a apporter assez de réponses.
Mais je me demande toujours si ma phrase est correcte? (voir plus haut)
++
155 résultats trouvés
Revenir à la recherche avancée
- 12 Nov 2006, 21:53
- Forum: ✯✎ Supérieur
- Sujet: A et B deux parties bornées de R, inf (A U B)?
- Réponses: 7
- Vues: 1195
Ai-je le droit de dire:
"A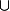 B étant l'ensemble formé par les éléments de A et les éléments de B, inf(A
B étant l'ensemble formé par les éléments de A et les éléments de B, inf(A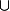 B)=inf(A) ou inf(B)" ?
B)=inf(A) ou inf(B)" ?
"A
- 12 Nov 2006, 20:52
- Forum: ✯✎ Supérieur
- Sujet: A et B deux parties bornées de R, inf (A U B)?
- Réponses: 7
- Vues: 1195
- 12 Nov 2006, 20:37
- Forum: ✯✎ Supérieur
- Sujet: A et B deux parties bornées de R, inf (A U B)?
- Réponses: 7
- Vues: 1195
A et B deux parties bornées de R, inf (A U B)?
Salut à tous! En cette fin de week end, j'ai à nouveau besoin de votre aide! Voici mon petit problème: A et B étant des parties bornées de \mathbb{R} Je dois determiner Inf(A \cup B) en fonction de Inf(A) et Inf(B). Pour ma part, je dirais que: -si Inf(A) Inf(B) alors Inf(A \cup B) = Inf(B) Mais je ...
- 12 Nov 2006, 20:04
- Forum: ✯✎ Supérieur
- Sujet: A et B deux parties bornées de R, inf (A U B)?
- Réponses: 7
- Vues: 1195
Je pense que je vais abandonner pour ce soir. Je suis vraiment pas à l'aise avec ces trucs là... En plus je commence vraiment à être crevé... lol! Bon bah je crois que y'a plus qu'à compter sur ma bonne étoile pour qu'il n'y ait pas ce genre de truc dans mon interro de demain... Enfin en tout cas, m...
- 09 Nov 2006, 22:05
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
Oki, merci bien! :lol4: Il me reste une question: (f est toujours bijective) x \in f(A) \Rightarrow f^{-1}(x) \in A Mon prof m'a dit que cette implication est fausse, mais je ne comprend pas pourquoi... Peux-tu m'expliquer? (avec un contre exemple si possible...) Merci d'avance! :we:
- 09 Nov 2006, 21:52
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
Donc, si je récapitule la chose:
Si f est bijective, alors l'équivalence que j'ai posé dans mon premier post est vraie, c'est ça?
Merci
Si f est bijective, alors l'équivalence que j'ai posé dans mon premier post est vraie, c'est ça?
Merci
- 09 Nov 2006, 21:37
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
Oui, je n'ai pas précisé que f était bijective, escusez moi...
J'ai beaucoup de mal avec ce genre de logique mathématique... :triste:
J'ai beaucoup de mal avec ce genre de logique mathématique... :triste:
- 09 Nov 2006, 21:24
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
- 09 Nov 2006, 21:15
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
- 09 Nov 2006, 21:12
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
Personne ne sait?
Si quelqu'un a la réponse, je veux bien qu'il me la donne parce que j'ai une interro de maths demain... :triste:
Merci d'avance!
Si quelqu'un a la réponse, je veux bien qu'il me la donne parce que j'ai une interro de maths demain... :triste:
Merci d'avance!
- 09 Nov 2006, 21:03
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
Salut à tous! Aujourd'hui, je me suis posé une petite question en révisant mon cours de logique. Si quelqu'un pouvait m'éclairer, ce serait super sympa! Voilà, je sais que: f^{-1}(x) \in f^{-1}(A) \Rightarrow x \in A Mais a-t-on la réciproque? C'est à dire: x \in A \Rightarrow f^{-1}...
- 09 Nov 2006, 20:07
- Forum: ✯✎ Supérieur
- Sujet: f^-1(x) dans f-1(A) => x dans A, réciproque vraie?
- Réponses: 16
- Vues: 1472
Il n'y a donc pas d'autre méthodes?
Pauvre de moi... :triste:
A moin que personne ne veuille me répondre telement la décomposition en élements simples c'est chiant, lol!
Personne n'a le courage de m'aider?
Pauvre de moi... :triste:
A moin que personne ne veuille me répondre telement la décomposition en élements simples c'est chiant, lol!
Personne n'a le courage de m'aider?
- 01 Nov 2006, 14:46
- Forum: ✯✎ Supérieur
- Sujet: Décomposition en élément simple d'une fraction, méthode plus
- Réponses: 1
- Vues: 1761
Décomposition en élément simple d'une fraction, méthode plus
Salut à tous! J'espère que vos vacances ce passe bien, du moin pour ceux qui en ont! Voilà, j'aurai besoin de votre aide aujourd'hui sur une décomposition d'une fraction rationelle en éléments simples. La voici: \frac{X^6}{(X^2+1)^2.(X+1)^2} Pour le moment, j'ai essayé le changement ...
- 01 Nov 2006, 13:25
- Forum: ✯✎ Supérieur
- Sujet: Décomposition en élément simple d'une fraction, méthode plus
- Réponses: 1
- Vues: 1761
Mince, je vien de m'apercevoir que c'est faux...
Bon bah je vais réessayer! Si quelqu'un a une méthode a me proposer, je suis prenant!
Merci!
Bon bah je vais réessayer! Si quelqu'un a une méthode a me proposer, je suis prenant!
Merci!
- 21 Oct 2006, 17:00
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
Bon, finalment j'ai réfléchi un peu et j'ai trouvé ça:
}+\frac{1}{2(X-1)}+\frac{1}{2(X-i)}-\frac{1}{2(X+i)})
C'est juste?
PS: j'ai utiliser un système, il faut procéder comme ça?
C'est juste?
PS: j'ai utiliser un système, il faut procéder comme ça?
- 21 Oct 2006, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
- 21 Oct 2006, 16:19
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
- 21 Oct 2006, 16:12
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
- 21 Oct 2006, 16:03
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
Je vais voir si j'ai bien compris:
Décomposer en éléments simples dans C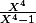
Je trouve:
(X-1)(X-i)(X+i)})
C'est juste?
Merci!
Décomposer en éléments simples dans C
Je trouve:
C'est juste?
Merci!
- 21 Oct 2006, 15:45
- Forum: ✯✎ Supérieur
- Sujet: Décomposer en éléments simples dans C et R
- Réponses: 10
- Vues: 2405
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
