13 résultats trouvés
Revenir à la recherche avancée
Bonjour, Pistes, 1)Soit I le milieu de [BC] x_I=\frac{x_B+x_C}{2} ( à calculer ) \vec{AI}(x_I-x_A,y_I-y_A) ( à calculer ) \vec{AG}(x_G-x_A,y_G-y_A)=(x_G-1,y_G-4) Vu que \vec{AG}=\frac{2}{3}\vec{AI} , on peut ainsi calculer les coordonnées de G Tu peux déterminer les cordonnée...
- 29 Mai 2009, 08:03
- Forum: ✎✎ Lycée
- Sujet: Probleme de mathematique
- Réponses: 2
- Vues: 556
Oui , c'est bon pour U2 , U3 , U4 ( et j'espère que tu as bien lu les sages conseils de Timothé Lefebvre )
- 20 Mai 2009, 17:51
- Forum: ✎✎ Lycée
- Sujet: c'est bon ou pas ?
- Réponses: 17
- Vues: 1070
Reprenons . U_n=U_1+(n-1)r ( c'est du cours , mais tu peux le trouver facilement) Tu remplaces U_1 par sa valeur 1550 et r par sa valeur -320 U_n=1550+(n-1)(-320) Tu développes : U_n=1550-320n+320 Donc : U_n=(1550+320)-320n Tu n'as plus qu'une addition à faire ...
- 20 Mai 2009, 09:41
- Forum: ✎✎ Lycée
- Sujet: c'est bon ou pas ?
- Réponses: 17
- Vues: 1070
Pas tout à fait...car ton "n" est mal placé...
Applique tout simplement la formule que je t'ai donné.
Applique tout simplement la formule que je t'ai donné.
- 20 Mai 2009, 09:25
- Forum: ✎✎ Lycée
- Sujet: c'est bon ou pas ?
- Réponses: 17
- Vues: 1070
- 20 Mai 2009, 08:58
- Forum: ✎✎ Lycée
- Sujet: c'est bon ou pas ?
- Réponses: 17
- Vues: 1070
r représente la raison de la suite arithmétique , c'est à dire ici r=45.
( rappel : dans une suite arithmétique , à partir du premier terme , on passe d'un terme au suivant en ajoutant une quantité constante : la raison )
( rappel : dans une suite arithmétique , à partir du premier terme , on passe d'un terme au suivant en ajoutant une quantité constante : la raison )
- 19 Mai 2009, 10:36
- Forum: ✎✎ Lycée
- Sujet: probleme suite arithmetique
- Réponses: 3
- Vues: 790
Bonjour, Je pense que si tu regardes ton cours , tu sauras faire... U_0=120 r=45 U_n=U_0+nr (c'est du cours ) Pour calculer U_1 , tu remplaces n par 1 dans la dernière formule écrite Pour calculer U_8 , tu remplaces n par 8 dans la dernière formule écrite Pour calculer U_{20} , tu remplaces n par 20...
- 19 Mai 2009, 10:17
- Forum: ✎✎ Lycée
- Sujet: probleme suite arithmetique
- Réponses: 3
- Vues: 790
Bonjour,
Il te suffit d'utiliser ta calculette.
Veille qu'elle soit en mode radians.
Utilise la fonction qui , en général , se note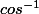
Il te suffit d'utiliser ta calculette.
Veille qu'elle soit en mode radians.
Utilise la fonction qui , en général , se note
- 19 Mai 2009, 09:35
- Forum: ✎✎ Lycée
- Sujet: Exercice : Produits Scalaires
- Réponses: 4
- Vues: 932
Bonjour, Tout d'abord : 3$x \ge 0 Asle , je vois une erreur dans ton premier calcul , qui doit te fausser toute la suite : AB=x+3 AC=AB+BC=x+3+x=2x+3 AC²=AD²+DC² (2x+3)²=100+DC² Finalement , DC²=(2x+3)²-100=4x²+9+12x-100= 4x²+12x-91 Pour la suite : AD²=AB²+BD² 100=(x+3)²+BD² DC²=BD²+BC² 4x²+12x-91=1...
- 29 Déc 2007, 10:41
- Forum: ✎✎ Lycée
- Sujet: [ Polynômes et géométrie ]
- Réponses: 8
- Vues: 781
Bonjour,
Aide pour le second,
Conditions d'existence : x>0 et -x+12>0 , c'est à dire : 0lnxx^2+x-12<0[/TEX]
Inéquation du second degré à résoudre sur ]0,12[
Après calculs , on trouve , pour ensemble des solutions :
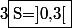
Aide pour le second,
Conditions d'existence : x>0 et -x+12>0 , c'est à dire : 0lnxx^2+x-12<0[/TEX]
Inéquation du second degré à résoudre sur ]0,12[
Après calculs , on trouve , pour ensemble des solutions :
- 29 Déc 2007, 10:10
- Forum: ✎✎ Lycée
- Sujet: inéquations de logarithme népérien
- Réponses: 3
- Vues: 930
Bonsoir, a) 3$aire(AA'B)=\frac{BA'\times AH}{2} 3$aire(AA'B)=\frac{1}{2}AB\times AA'\times \sin \widehat{BAA'} De même , 3$aire(AA'C)=\frac{CA'\times AH}{2} 3$aire(AA'C)=\frac{1}{2}AC\times AA'\times \sin \widehat{CAA'} (AA') ét...
- 28 Déc 2007, 23:54
- Forum: ✎✎ Lycée
- Sujet: Points remarquables d'u triangle , barycentres
- Réponses: 3
- Vues: 935
Bonsoir, Je te réponds au premier exercice . OK pour tes calculs pour trouver X²-X+2=0 C'est après que ça ne va pas. Il faut retourner à x 1er cas : 4$X=1x+\frac{1}{x}=1x^2+1=xx^2-x+1=0 Equation du second degré : Discriminant x+\frac{1}{x}=2x^2+1=2xx^2-2x+1=0[/TEX] Tu reconnais 4$(x-1)^2=0x-...
- 28 Déc 2007, 19:52
- Forum: ✎✎ Lycée
- Sujet: Dm barycentres et trinomes 1s
- Réponses: 5
- Vues: 624
Bonjour,
Soit C1=31951 ( en 2004)
Soit C0 = ? (en 1998)
C1=C0+155%C0
C1=C0(1+1.55)
C1=2.55 C0
Tu remplaces C1 par sa valeur et tu en déduis C0
Soit C1=31951 ( en 2004)
Soit C0 = ? (en 1998)
C1=C0+155%C0
C1=C0(1+1.55)
C1=2.55 C0
Tu remplaces C1 par sa valeur et tu en déduis C0
- 28 Déc 2007, 14:51
- Forum: ✎✎ Lycée
- Sujet: DM de maths ==>Taux de variation
- Réponses: 2
- Vues: 659
- 13 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
