Forum de Mathématiques: Maths-Forum

Bonjour

merci GaBuZoMeu pour cette formule dite de la crosse hockey (celle avec le sigma), j'avais du connaître mais je l'avais oubliée.

https://fr.wikipedia.org/wiki/Formule_d ... _de_Pascal

Hum catamat ! Comment veux-tu trouver un entier naturel k tel que -k \ln(3) \geq a quand a>0 ? Ce n'est pas difficile à réparer, je te laisse y penser. Oui merci GaBuZoMeu, après avoir posté je me suis douté qu'il y avait un problème à ce niveau.... Je pense que l'on choisit k entier nature...

Bonjour, de façon à faire avancer le sujet je propose ceci pour le cas "-e dans E" , en espérant ne pas faire trop d'erreurs... D'abord une remarque sur ce résultat précédent : Alors il existe un (unique) entier naturel \ell tel que -k\ln(3)+\ell e\leq a<-k\ln(3)+(\ell+...

Bonjour Je pense qu'imod a voulu dire que \frac{an}b-\lfloor\frac{an}b\rfloor peut approcher la partie fractionnaire de \frac yb à volonté Donc \frac{an}b-\lfloor\frac{an}b\rfloor approche \frac yb-\lfloor\frac{y}b\rfloor ou \frac{an}b-\lfloor\frac{an}b\rfloor +\lfloor\frac{y}b\rfloor approche \frac...

Bonjour

Je pense que l'exercice 2 du lien suivant devrait t'éclairer

https://perso.eleves.ens-rennes.fr/peop ... de%20R.pdf

Ben 314 m'a devancé, mais bon j'envoie quand même ce que j'écrivais En fait il y a deux N_2 possibles Le premier qui a autant de chiffres que N_3 ( n chiffres donc), je le note N_2 Le second qui a un chiffre de plus , notons le N'_2 , on a N'_2*10N_2+a où a est un chiffre compris entre 0 et ...

par ex : N_1=34812 et N_3=347 N_2=348 1 N_2>10N_3 N_2=348 car 348 \ge 347 10N_3=3470>N_2=348 ce n'est pas ça ? Certes , ce que je voulais dire c'est que pour cet exemple; on a : N_1=100N_2+10x_1+x_0 et non pas N_1=10N_2+x_0 comme vous le définissiez plus haut Par contre je suis OK pour dire que le ...

Bonjour Il faudrait un énoncé clair indiquant ce que l'on suppose et ce que l'on cherche à démontrer... Il est évident que si N_2 est défini comme N_1=10 N_2 + x_0 où x_0 est le chiffre des unités de N_1 , avec un N_3 quelconque, on n'aura pas nécessairement N_2 / N_3 <10, par ex : N_1=34812 et N_3=...

Bonjour Au sujet du calcul de Gabuzomeu, merci de l'avoir fait il est très intéressant. Je l'ai refait et je trouve le même résultat. J'apporte juste une précision, pour le dl de ln(1+x) au voisinage de 0, il faut le prendre à l'ordre 2, au moins, pour avoir un résultat utilisable ou alors utiliser ...

Merci beaucoup Ben314

Il fallait donc partir du morphisme non pas de la surjectivité comme je faisais !

Bonjour Le forum étant plutôt calme, j'en profite pour poser une question, désolé si c'est trivial mais pour moi cela ne l'est pas. J'ai compris pourquoi x²y=yx² mais comment en déduit on la commutativité ? Faut il démontrer que tout élément de G peut s'écrire sous forme de carré ? La seule chose qu...

Bonjour Vam
Nouveau post à supprimer, merci
lycee/real-girls-for-private-relationships-t283872.html

Bonjour

Dans la formule : Indice endurance = (% de VMA maintenu pendant la course – 100) / ln (temps de course en minute / 6)
le temps dans le log est exprimé en minutes, il s'agit donc de 60T si T est en heures.
On trouve bien -5.55

Je sais que tu as écrit V'(x) le problème c'est que c'est faux !!

Il manque la dérivée de w qui est w'(x)=1/x

Bonjour

Le problème c'est la dérivée de v
v est du type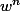 sa dérivée est
Tu as oublié w'...

Il faut le vérifier pour n=0 Ensuite l'IPP permet de démontrer l'hérédité au passage on obtient une relation de récurrence pour les polynômes P_n C'est : P_n(x)=x^n+nP_{n-1}(x) On peut donc trouver les premiers termes de la suite des P_n Par ex P_4(x)=x^4+4x^3+12x^2+24x+24 Ce...

Bonjour Amari Personnellement je démontrerais par récurrence que F_n(x)=-e^{-x+1}P_n(x) où P_n(x) est un polynôme de degré n. Puis je chercherais une relation de récurrence pour la suite (P_n) de façon à trouver l'expression de P_n(x) Mais bon Gabuzomeu aura s...

Bonjour
Pour la proba de "U=k" on a soit "X=k" et "Y supérieur à k" soit "Y=k" et "X supérieur à k",
mais attention ces deux événements ne sont pas incompatibles donc on doit retrancher leur intersection. On obtient bien le résultat annoncé.

Bonjour Le problème semble ne pas avoir de solution exacte, mais on peut trouver de bonnes valeurs approchées, c'est à dire des nombres a, b et c pour lesquels les trois probas sont presque égales. Par ex : a=3, b=4 et c=6 p(A)=3/13 soit environ 0.2308 p(B)= \frac{4}{13}\times\frac{3}{12}+\frac{6}{1...

Ton calcul correspond à il faut ensuite le multiplier par p(U2) soit 1/2 (si le choix des urnes est équiprobable).