Probabilité loi géométrique

[briwa]

Bonjour tout le monde j'espère que vous allez bien. Le semestre dernier j'avais un examen de probabilités il y avait un exercice où je ne savais même pas par où commencer. Quelqu'un veut bien me donner des pistes s'il vous plait?
Exercice 2. Soit X et Y deux variables aléatoires indépendantes qui suivent la loi géométrique G(p) où p appartient a ]0, 1[. on pose Z = X +Y, U = min(X,Y) et V = max(X, Y).
1) Pour tout entier k appartient a N*, calculer P(X >= k).
2) Déterminer les lois de U et V.
Indication: On doit trouver que U vérifie la loi géométrique de paramètre (1-(1- p)^2).
3) Déterminer la loi de Z.

[GaBuZoMeu]

Bonjour,
Connais-tu la signification de la loi géométrique de paramètre ? C'est le nombre d'épreuves de Bernoulli indépendantes de paramètre pour obtenir le premier succès (revois ton cours pour vérifier !)
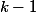L'évènement , ça veut dire que les premières épreuves sont ratées. Probabilité ?

[catamat]

Bonjour
Pour la proba de "U=k" on a soit "X=k" et "Y supérieur à k" soit "Y=k" et "X supérieur à k",
mais attention ces deux événements ne sont pas incompatibles donc on doit retrancher leur intersection. On obtient bien le résultat annoncé.

[GaBuZoMeu]

Bonsoir,
C'est sans doute plus simple de commencer par s'intéresser à .

[briwa]

Bonsoir et merci pour vos réponses! Pour être honnête cela fait un petit moment que je n'ai pas revu le cours mais je voulais poser la question avant d'oublier. J'espère pouvoir revenir dessus le plus vite possible pour réessayer et je reviendrais cette fois (je l'espère) avec une vraie tentative. Merci encore!