Bonjour,
Voici comment je vois les choses.
Une matrice est associée à une application linéaire.Dans le cadre des matrices (ou des endomorphismes d’un espace de dimension finie), les résultats sur les matrices sont analogues avec les résultats sur les endomorphismes d’un espace de dimension fini.
981 résultats trouvés
Revenir à la recherche avancée
- 01 Juin 2025, 11:15
- Forum: ✯✎ Supérieur
- Sujet: convergence uniforme pour des matrices
- Réponses: 5
- Vues: 705
Re: convergence uniforme pour des matrices
Bonjour,
Vous avez une somme de Matrice donc la convergence de cette somme à un sens : on cherche à savoir vers quelle matrice converge cette somme de matrice et de quelle manière elle converge le cas échéant.
donc la convergence de cette somme à un sens : on cherche à savoir vers quelle matrice converge cette somme de matrice et de quelle manière elle converge le cas échéant.
Vous avez une somme de Matrice
- 31 Mai 2025, 22:06
- Forum: ✯✎ Supérieur
- Sujet: convergence uniforme pour des matrices
- Réponses: 5
- Vues: 705
Re: Echec L3 maths fonda
Bonjour,
Essayez de discuter avec les professeurs pour savoir ce qu'il pense des raisons de vos résultats cette année.
Demandez leurs des conseils pour réviser cet été si vous redoublez afin de bien aborder la rentrée.
Essayez de discuter avec les professeurs pour savoir ce qu'il pense des raisons de vos résultats cette année.
Demandez leurs des conseils pour réviser cet été si vous redoublez afin de bien aborder la rentrée.
- 24 Avr 2025, 17:29
- Forum: ➳ Orientation
- Sujet: Echec L3 maths fonda
- Réponses: 1
- Vues: 207
Re: dérivée d'une fonction composée
Oups,oui vous avez raison.
- 12 Fév 2025, 21:37
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 2676
Re: dérivée d'une fonction composée
Pour la dérivée dt/dx je pense que c'est 4x au numérateur.
- 12 Fév 2025, 18:57
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 2676
Re: dérivée d'une fonction composée
Bonjour,
vous avez :

donc :

vous avez :
donc :
- 12 Fév 2025, 18:55
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 2676
Re: Une suite positive
oui, je vois ce que vous me dites et vous avez raison.
- 07 Jan 2025, 12:37
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
pour moi u1 est obtenu pour k=n-1
- 07 Jan 2025, 10:50
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
Bonjour,
@catamat , parce que est une somme de terme. Le terme correspondant à la valeur k=n+1, est celui avec
est une somme de terme. Le terme correspondant à la valeur k=n+1, est celui avec  car pour k=n+1 ,
car pour k=n+1 ,  . Si le terme pour k=n+1 est extrait de la somme alors il ne reste que n termes donc k varie de 1 à n.
. Si le terme pour k=n+1 est extrait de la somme alors il ne reste que n termes donc k varie de 1 à n.
@catamat , parce que
- 06 Jan 2025, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
Super, vous avez osez,c'est top et vous avez trouvé. pour ma part j'avais pris un autre chemin pour trouver,le voici (sauf erreur de ma part) : u_{n+1}=-\dfrac1{n+1}\sum_{k=1}^{n+1} \dfrac{u_{n+1-k}}{k+1} décomposition en 2 éléments,une pour k=n+1 et l'autre pour n allant de k=1 à n u_{n+1}=-\dfrac1...
- 05 Jan 2025, 22:08
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: intégrale définie
pour ma part, j'ai conduit le calcul en posant ( j'ai peut-être tort) :

A+B-C=0 ( je n'ai pas calculé A,B et C)
je trouve ( sauf erreur de ma part) : A ln(2) - (B-C) ln(|-a|).
A+B-C=0 ( je n'ai pas calculé A,B et C)
je trouve ( sauf erreur de ma part) : A ln(2) - (B-C) ln(|-a|).
- 05 Jan 2025, 21:50
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2002
Re: Une suite positive
u_{n+1}=-\dfrac1{n+1}\sum_{k=1}^{n+1}\dfrac{u_{n+1-k}}{k+1} transformez u_{n+1} en une somme de 2 éléments, une pour k=n+1 et l'autre pour n allant de k=1 à n. J'ai du mal à vous comprendre, vous êtres sauf erreur de ma part en études supérieures, vous ne montrez aucun de vos essais pour résoudre l...
- 05 Jan 2025, 20:00
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
une précision il faut démontrer que  est positif.
est positif.
- 05 Jan 2025, 15:41
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
Pour vérifier par récurrence une propriété : 1)La propriété ( ici u_n >0 ) est initialisée à partir du premier rang n >1, c'est-à-dire : u_n=-\dfrac1n \sum_{k=1}^{n}\dfrac{u_{n-k}}{k+1} pour n=1 on a u_1=- \sum_{k=1}^{1}\dfrac{u_{1-k}}{k+1}}= \dfrac12 >0 donc la propriété est vraie n=1 2) hypothèse ...
- 05 Jan 2025, 15:29
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Une suite positive
Par récurrence, sauf erreur de ma part cela fonctionne.
- 05 Jan 2025, 14:05
- Forum: ✯✎ Supérieur
- Sujet: Une suite positive
- Réponses: 15
- Vues: 1256
Re: Bonne année 2025
Bonsoir à tous et très bonne année 2025 avec la santé et du bonheur .










2025










2025
- 04 Jan 2025, 20:40
- Forum: ☕ Coin café
- Sujet: Bonne année 2025
- Réponses: 9
- Vues: 804
- 04 Jan 2025, 20:10
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2002
Re: intégrale définie
Bonjour, on a une équation du troisième degré de la forme x^3 + px + q = 0 avec q et p réels dont on connait une racine x_1 à savoir a et p=q=1. Sauf erreur de ma part en utilisant la méthode de méthode de Bombelli et en disant que x_1 =a on obtient les autres racines : x_2+x_3=-x_1=-a et x_2 . x_3=...
- 04 Jan 2025, 17:26
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2002
Re: distribution équation différentielle
Bonjour,
 est la distribution de Dirac.
est la distribution de Dirac.
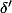 est la dérivée première de la distribution de Dirac.
est la dérivée première de la distribution de Dirac.
- 18 Nov 2024, 16:12
- Forum: ✯✎ Supérieur
- Sujet: distribution équation différentielle
- Réponses: 5
- Vues: 775
Re: Bon anniversaire à Capitaine Nuggets
Bonjour,
Je trouve très sympa de souhaiter les anniversaires. Alors
 à Capitaine Nuggets
à Capitaine Nuggets
Je trouve très sympa de souhaiter les anniversaires. Alors
 à Capitaine Nuggets
à Capitaine Nuggets- 14 Nov 2024, 18:34
- Forum: ☕ Coin café
- Sujet: Bon anniversaire à Capitaine Nuggets
- Réponses: 3
- Vues: 630
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
