74 résultats trouvés
Revenir à la recherche avancée
Re: Valeurs propres d'un endormorphisme
Je regarderai ! Merci !
- 07 Oct 2021, 09:54
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Oui, dis comme ça... Donc n=3 et a_n-1 =0. Voilà qui rend la question plus simple !!
Je finis l'exercice demain !
Merci beaucoup pour tes précieux éclairages !
Je finis l'exercice demain !
Merci beaucoup pour tes précieux éclairages !
- 05 Oct 2021, 20:16
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Bien sûr, a_n est non-nul, ce qui garantit n=3. Mais si a_n-1 est aussi non-nul, alors on tombe sur une absurdité, non ?
- 05 Oct 2021, 17:29
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Si 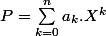 , alors
, alors =a_n.(n-3).X^{n+2}+a_{n-1}.X^{n+1}.(n-4)+...)
Comme P, et donc f(P), sont de degré n, alors on obtient les deux equations suivantes :=0) et
et =0) , ce qui est absurde... Où est l'erreur ?
, ce qui est absurde... Où est l'erreur ?
Comme P, et donc f(P), sont de degré n, alors on obtient les deux equations suivantes :
- 05 Oct 2021, 16:45
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Okay je regarde ça et je reviens !
- 05 Oct 2021, 14:53
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Excuse-moi pour la faute de frappe malheureuse.
Je te suis bien mais je ne vois pas vraiment comment faire surgir lesdites contraintes...
Merci pour ton aide.
Je te suis bien mais je ne vois pas vraiment comment faire surgir lesdites contraintes...
Merci pour ton aide.
- 05 Oct 2021, 14:45
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Si P est vecteur propre de f, alors on a f(P)=lambda*P, et donc les degrés sont les mêmes.
Je ne vois pas où tout cela peut nous amener...
Je ne vois pas où tout cela peut nous amener...
- 05 Oct 2021, 13:52
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: Valeurs propres d'un endormorphisme
Bonsoir à toi,
On peut dire que si P est de degré d, alors l'on a : deg(f(P)) inférieur ou égal à d+2. Je ne vois pas comment poursuivre...
On peut dire que si P est de degré d, alors l'on a : deg(f(P)) inférieur ou égal à d+2. Je ne vois pas comment poursuivre...
- 03 Oct 2021, 17:55
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Valeurs propres d'un endormorphisme
Bonjour à tout le monde ! Voilà l'énoncé que je n'arrive pas à résoudre ! Déterminer les valeurs propres de l'endomorphisme de R[X] défini par f(P)=(X^3+X)P'-(3X^2-1)P. Comme l'espace considéré n'est pas de dimension finie, on ne peut pas passer par la matrice et le polynôme caractéristique et on ch...
- 03 Oct 2021, 17:35
- Forum: ✯✎ Supérieur
- Sujet: Valeurs propres d'un endormorphisme
- Réponses: 15
- Vues: 512
Re: REPRISE ETUDES
Je suis en Licence 2. Et bien, il s'agit de cours universitaires standards, le niveau n'est pas particulièrement avancé (mais pas particulièrement faible non plus). Les exercices proposés sont très souvent des exercices d'application uniquement. Enfin, comme partout, il y a des profs motivés et d'au...
- 07 Sep 2021, 08:55
- Forum: ✯✎ Supérieur
- Sujet: REPRISE ETUDES
- Réponses: 11
- Vues: 1136
Re: REPRISE ETUDES
N'hésite pas si tu as des questions 
- 24 Aoû 2021, 13:56
- Forum: ✯✎ Supérieur
- Sujet: REPRISE ETUDES
- Réponses: 11
- Vues: 1136
Re: Logiciel Sage
C'est bon problème résolu 
- 23 Aoû 2021, 16:35
- Forum: ✯✎ Supérieur
- Sujet: Logiciel Sage
- Réponses: 4
- Vues: 371
Re: REPRISE ETUDES
Bonjour, Alors, reprenons point par point la réponse d'azf qui manque de pertinence. Tout d'abord, être attiré par le fun et la beauté des maths n'est en aucun cas un problème bien au contraire, et n'exprime en rien un manque d'amour du travail bien fait. Les maths sont certes vieilles, mais en per...
- 22 Aoû 2021, 19:31
- Forum: ✯✎ Supérieur
- Sujet: REPRISE ETUDES
- Réponses: 11
- Vues: 1136
Re: Logiciel Sage
L'indentation n'est pas passée mais il n'y a pas de problème de ce côté-là !
- 22 Aoû 2021, 19:28
- Forum: ✯✎ Supérieur
- Sujet: Logiciel Sage
- Réponses: 4
- Vues: 371
Re: Logiciel Sage
Bonjour à toi ! Merci pour ta réponse et excuse-moi pour la mienne qui est un peu tardive ! J'ai un problème avec le code suivant : A=matrix([[0,1],[1,1]]) b=vector([0,1]) def fibi(n): if n==0 or n==1:return n else: b=A^(n-1)*b return b[1] fibi(5) Il ne renvoie qu'un message d'erreur ! Je ne vois pa...
- 22 Aoû 2021, 19:27
- Forum: ✯✎ Supérieur
- Sujet: Logiciel Sage
- Réponses: 4
- Vues: 371
Re: REPRISE ETUDES
Je suis dans une grande école parisienne et je fais des maths pour m'amuser dans le cadre d'une licence avec le CTU de Besançon ! Tu (vous ?) peux (pouvez ?) y aller les yeux fermés, c'est très bien, même si le niveau des cours n'est pas exceptionnel !
- 22 Aoû 2021, 19:25
- Forum: ✯✎ Supérieur
- Sujet: REPRISE ETUDES
- Réponses: 11
- Vues: 1136
Logiciel Sage
Bonjour !
Quelqu'un connaitrait-il le logiciel de calcul formel Sage ?
Il y a une petite chose qui m'échappe !
Bien à vous,
Frandom94
Quelqu'un connaitrait-il le logiciel de calcul formel Sage ?
Il y a une petite chose qui m'échappe !
Bien à vous,
Frandom94
- 04 Aoû 2021, 15:02
- Forum: ✯✎ Supérieur
- Sujet: Logiciel Sage
- Réponses: 4
- Vues: 371
Re: Indépendance linéaire
Oui, j'ai bien la même chose. Merci beaucoup !
- 08 Juin 2021, 22:19
- Forum: ✯✎ Supérieur
- Sujet: Indépendance linéaire
- Réponses: 13
- Vues: 406
Re: Indépendance linéaire
Ok super ! Merci beaucoup !
- 30 Mai 2021, 09:12
- Forum: ✯✎ Supérieur
- Sujet: Indépendance linéaire
- Réponses: 13
- Vues: 406
Re: Indépendance linéaire
Oui, j'imagine qu'on est dans un R-espace vectoriel même si ça n'est pas précisé dans l'énoncé.
Par curiosité, je me demandais juste si on pouvait passer sans déterminant. En appliquant la définition par exemple...
Par curiosité, je me demandais juste si on pouvait passer sans déterminant. En appliquant la définition par exemple...
- 30 Mai 2021, 07:35
- Forum: ✯✎ Supérieur
- Sujet: Indépendance linéaire
- Réponses: 13
- Vues: 406
- 74 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
