27 résultats trouvés
Revenir à la recherche avancée
Excuse moi je dois avoir du mal mais j'arrive pas à prouver le G continue sur le disque compact est bornée et atteint ses bornes ...j'ai essayé en introduisant les applications partielles mais non :triste: et puis qu'est-ce que ça veut dire "compact"? j'ai cru comprendre en googlisant que ...
- 03 Mai 2008, 15:02
- Forum: ✯✎ Supérieur
- Sujet: Fonctions de deux variables
- Réponses: 6
- Vues: 1005
Merci! Juste une question: pour le minimum de g, ça marche comme pour les fonctions à une seule variable, si g est bornée et continue, elle atteint son minimum? Si oui, je montre ça comment? Et puis j'ai aussi un doute: f de classe  , ça implique f de classe
, ça implique f de classe 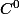 ?
?
- 03 Mai 2008, 10:46
- Forum: ✯✎ Supérieur
- Sujet: Fonctions de deux variables
- Réponses: 6
- Vues: 1005
Fonctions de deux variables
Bonsoir à tous! Voilà, j'ai un exercice sur les fonctions de deux variables qui me pose problème...Voici l'énoncé: Soient D=\{(x,y)\in\mathbb{R}^2,x^2+y^2\le 1\} et f\in(D,\mathbb{R}) telle que \forall (x,y)\in D,|f(x,y)]\le1 . Montrer que: \exists (x_0,y_0)\i...
- 02 Mai 2008, 20:18
- Forum: ✯✎ Supérieur
- Sujet: Fonctions de deux variables
- Réponses: 6
- Vues: 1005
- 06 Jan 2008, 21:56
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
Non non, jamais eu de cours sur les polynômes cette année (d'ailleurs apparemment on n'a pas abordé le programme dans l'ordre habituel)...
- 06 Jan 2008, 14:27
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
- 06 Jan 2008, 13:56
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
- 06 Jan 2008, 11:08
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
En fait le problème c'est qu'on n'a absolument pas traité de polynômes en cours pour l'instant donc s'il faut que je démontre aussi le résultat sur les racines...on n'est pas sorti de l'auberge (même si je peux recopier la démo du deschamps c'est vrai) :lol2:
- 05 Jan 2008, 21:19
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
- 05 Jan 2008, 21:06
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
- 05 Jan 2008, 21:02
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
Euh j'ai pas très bien compris ce que tu proposes...récurrence forte? mais X n'est pas nécessairement un entier, si?...
- 05 Jan 2008, 20:47
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
Espace vectoriel
Bonsoir, Je suis bloquée sur un exo sur les espaces vectoriels depuis un certain temps...bref un ptit coup de main serait le bienvenu! Voici le sujet: Soit \Delta : \mathbb {C \rightarrow C} défini par: \Delta (P)(X)=P(X+1)-P(X) . On définit \Delta^0=Id_{\mathbb{C}[X]...
- 05 Jan 2008, 19:40
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 16
- Vues: 792
- 12 Nov 2007, 23:21
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
Excuse moi mais j'ai pas compris comment tu procèdes pour les trois dernières étapes de ta minoration...
PS: Sinon tize je sais pas du tout si "c'est vrai ça" mais ça m'aurait arrangé^^
PS: Sinon tize je sais pas du tout si "c'est vrai ça" mais ça m'aurait arrangé^^
- 12 Nov 2007, 23:00
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
bitonio a écrit:Pas grave, on est tous passé par là ^^ (et encore moi j'en suis pas sorti :triste: !)
Si t'avais lu mon édition tu verrais que j'ai toujours pas percuté le truc :ptdr:
Tu la montres comment l'inégalité avec la valeur absolue?
- 12 Nov 2007, 22:03
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
- 12 Nov 2007, 22:00
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
- 12 Nov 2007, 21:55
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
- 12 Nov 2007, 21:44
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
Mais ça me permet pas d'en déduire que \sum|ln|1+u_n|| converge...non? Ce que j'aimerai faire c'est montrer que |ln|1+u_n||\le \ln(1+|u_n|)\sim \|u_n| pour en déduire du théorème sur les séries à termes équivalents positifs que \sum ln(1+|u_n|) converge donc \sum|ln|1+u_n|| converge...
- 12 Nov 2007, 00:57
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
- 12 Nov 2007, 00:11
- Forum: ✯✎ Supérieur
- Sujet: Convergence absolue d'une série
- Réponses: 17
- Vues: 1846
- 27 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
