Forum de Mathématiques: Maths-Forum

Nightmare a écrit:Exact! Tout ce que je dis valais pour R tout entier, mais sur [0,1] je suis d'accord avec ton raisonnement.

Donc l'inf c'est 1. Non ?

Tu es sur de tes minorants? N'oublie pas qu'on est sur R tout entier, et qu'on a des négatifs. 1/(-1) est inférieur à 1 par exemple donc 1/x n'est pas minorée par 1 sur Q. Non..On est sur [0,1]...on veut les bornes juste sur cet intervalle..x appartient à [0,1]...il n'y a pas de négatifs...c'est po...

Salut, Pour le sup et le max, dire que 1/x n'est pas majorée n'est pas suffisant, il faut préciser sur Q. Par exemple, si je prends f(x)=1/x si x appartient à N* et x+2 sinon, l'argument n'est plus bon. Pour l'inf et le min, vois-tu déjà d'éventuels candidats? Autrement dis, vois-tu une valeur tell...

Bonjour ! soit une fonction f définie sur [0,1] telle que f(x)=1/x si x n'appartient pas à Q et f(x)= x+2 si x appartient à Q Il m'est demandé de déterminer le Sup Inf Max Min de f sur [0,1] puisque 1/x n'est pas majorée, le sup et le max de f n'existent pas...x+2 est bornée...1/x est minorée par 1....

busard_des_roseaux a écrit:bonjour

soit l'inégalité

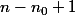
multiplie les inégalités membres à membres. c'est télescopique

Ah Ouais !!... C'est Vrai...Merci :happy2:

Salut Tout le Monde...Voila Mon Problème : Soit (Un) et (Vn) 2 suites réelles à termes strictement positifs tel que on a : \frac{U{n+1}}{U{n}}\leq \frac{V{n+1}}{V{n}} A partir d'un certain rang...(n+1 Dans l'indice de U et V) Il Faut Que Je Démontre L'implication suivante : \lim{V{n}}=0\Rightarrow \...

Salut, On pose p = E(nx) et on effectue la division euclidienne de p par n : p = nq + r,\,0\leq r \leq n -1. Calcule E\left(x+\displaystyle \frac{k}{n}\right) pour 0\leq k \leq n-r-1 et pour n-r\leq k \leq n-1. EDIT : L'égalité à montrer est plutôt \displaystyle \sum^{n-1}_{k=0} E\l...

arnaud32 a écrit:es tu deja sure que c'est vrai?
ex x=1/n et k= n-1

J'ai pas Compris ton exemple ???...k Varie de 0 juska n-1 dans une somme

Bonjour Tout le monde...Je Veux Bien Démonter Cette Egalité :

Sigma de k=0 jusqu'a n-1 des E((x+k)/n) = E(x)

Ca n'a pas marché avec les encadrements j'ai beau essayé :mur:

merci Bien !!

cet exercice s'est posé dans un controle de maths et je veux vos réponses pour les comparer aux mienne et merci d'avance soit EABCD une pyramide dont la base et le rectangle ABCD et la hauteur AE tel que: AD=3cm AE=5cm AB=4cm I est le milieu de EB J est le milieu de EC 1- construire la figure 2- Cal...