Partie Entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
liverpool
- Membre Naturel
- Messages: 10
- Enregistré le: 21 Mai 2007, 20:25
-
 par liverpool » 04 Nov 2011, 16:30
par liverpool » 04 Nov 2011, 16:30
Bonjour Tout le monde...Je Veux Bien Démonter Cette Egalité :
Sigma de k=0 jusqu'a n-1 des E((x+k)/n) = E(x)
Ca n'a pas marché avec les encadrements j'ai beau essayé :mur:
merci Bien !!
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2011, 16:45
par arnaud32 » 04 Nov 2011, 16:45
es tu deja sure que c'est vrai?
ex x=1/n et k= n-1
-
liverpool
- Membre Naturel
- Messages: 10
- Enregistré le: 21 Mai 2007, 20:25
-
 par liverpool » 04 Nov 2011, 16:56
par liverpool » 04 Nov 2011, 16:56
arnaud32 a écrit:es tu deja sure que c'est vrai?
ex x=1/n et k= n-1
J'ai pas Compris ton exemple ???...k Varie de 0 juska n-1 dans une somme
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2011, 17:09
par arnaud32 » 04 Nov 2011, 17:09
pardon j'ai mal lu ta formule
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2011, 17:14
par arnaud32 » 04 Nov 2011, 17:14
x=n
E(x)=n
(x+k)/n=1+k/n avec 0=< k/n <1 donc E((x+k)/n)=1
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 04 Nov 2011, 17:38
par manoa » 04 Nov 2011, 17:38
x et n c'est qui?
-
Anonyme
 par Anonyme » 04 Nov 2011, 17:57
par Anonyme » 04 Nov 2011, 17:57
liverpool a écrit:Bonjour Tout le monde...Je Veux Bien Démonter Cette Egalité :
Sigma de k=0 jusqu'a n-1 des E((x+k)/n) = E(x)
Ca n'a pas marché avec les encadrements j'ai beau essayé :mur:
merci Bien !!
Bonjour
Est ce que ta question dans ton exercice est :
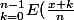=E(x))
??
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Nov 2011, 18:07
par Zweig » 04 Nov 2011, 18:07
Salut,
On pose
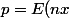)
et on effectue la division euclidienne de

par

:
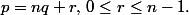
Calcule
)
pour

et pour

EDIT : L'égalité à montrer est plutôt
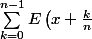 = E(nx))
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Nov 2011, 19:10
par Zweig » 04 Nov 2011, 19:10
Ou bien, au choix :
On pose
 = \displaystyle \sum^{n-1}_{k=0} E\left(x+\displaystyle \frac{k}{n}\right) - E(nx))
. On remarque l'identité suivante :
 = f\left(x+\frac{1}{n}\right))

est donc 1/n-périodique. Il suffit donc d'étudier f sur un intervalle d'amplitude 1/n, disons sur l'intervalle [0, 1/n]. Il est clair que sur cet intervalle,
 = 0)
, ce qui conclut.
-
liverpool
- Membre Naturel
- Messages: 10
- Enregistré le: 21 Mai 2007, 20:25
-
 par liverpool » 04 Nov 2011, 19:55
par liverpool » 04 Nov 2011, 19:55
Zweig a écrit:Salut,
On pose
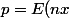)
et on effectue la division euclidienne de

par

:
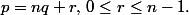
Calcule
)
pour

et pour

EDIT : L'égalité à montrer est plutôt
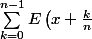 = E(nx))
Ah Je Vois...Donc L'égalité Que Je Dois Démontrer n'était qu'un cas particulier celui de x/n...Mercii ;D
-
Anonyme
 par Anonyme » 04 Nov 2011, 20:03
par Anonyme » 04 Nov 2011, 20:03
Ben oui merci Zweig........ avec un Z comme....
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 06 Nov 2011, 19:57
par Zweig » 06 Nov 2011, 19:57
comme ? :hein:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
