Forum de Mathématiques: Maths-Forum

D'accord mais quelle est la primitive de exp(x)(acos(x) + bsin(x))

Bonjour et merci à tous pour votre attention l'équation est la suivante : y'(x) + y(x) = cos x + sin x Je trouve pour l'équation homogène : yh = Kexp(-x) Avec la méthode de la variation de la constante pour la solution particulière j'ai donc : yp = K(x)exp(-x) et donc y'p = K'(x)exp(-x) -K(x)exp(-x)...

Super j'ai trouvé ! merci infiniment !

Et pour K'(x) =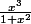 vous avez une idée de quelle primitive il s'agit ?

En fait je sais que c'est ça puisque l'énoncé donne juste les réponses finale ici y(t) = 1/x + Kln(x) mais comment parvient-on à ce fameux 1/x en partant de mon K'(x) car c'est ça qu'on nous demandera au partiel finale
Merci pour ton aide

Bonjour, je résous actuellement une équation différentielle avec la méthode de variation de la constante. L'équation est la suivante : (xln(x)) y'(x) - y(x) = - \frac{1}{x} (ln(x)+1) j'ai trouvé y_H = Kln(x) Ensuite je suis bloqué à K'(x) = - \frac{(ln(x) + 1)}{x^{2}l...

Il est possible que cela se fasse en deux fois, d'abord u = x v'=racine(4-x)
tu fais tes calcules puis rebelote u = résultats que tu as trouvé et v' = sin x
essaye et dit moi si sa marche, ce n'est qu'une idée je ne l'ai pas essayé

Bonjour tout le monde, et merci de votre aide d'avance. J'essaye de m'avancer en maths en ce moment, seulement je suis bloquer sur une question qui je suis sûr est toute bête mais je ne vois pas comment faire. Voila l'équation différentielle : (xln(x)) y'(x) - y(x) = - \frac{1}{x} (ln(x)+1) je suis ...