25 résultats trouvés
Revenir à la recherche avancée
Volume
Bonjour, Ma question est la suivante: En utilisant les cordonnées sphériques, calculer le volume de la région Q qui est en dessous de z=8-x^2-y^2 , au-dessus de z=-\sqrt{4x^2+4y^2} et à l'intérieur de x^2+y^2=4. Les cordonnés sphériques sont (\rho, \theta, \phi) avec \rho : distance à l'orig...
- 28 Avr 2022, 09:22
- Forum: ✯✎ Supérieur
- Sujet: Volume
- Réponses: 0
- Vues: 232
Re: comparaison de deux suites
@mathelot, merci beaucoup pour votre réponse.
- 17 Déc 2021, 19:22
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
J'ai pas bien saisi l'argument utilisé.
Si a_0 >b_0, quel est l'argument utilisé pour montrer la convergence des suites ? car dans ce cas, je pense que la suite, par exemple,( a_n) n'est pas croissante.
Me trompe-je ?
Si a_0 >b_0, quel est l'argument utilisé pour montrer la convergence des suites ? car dans ce cas, je pense que la suite, par exemple,( a_n) n'est pas croissante.
Me trompe-je ?
- 11 Déc 2021, 17:44
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
Ma question est la suivante: les suites (a_n) et (b_n) sont-elles convergentes? peu n'importe 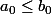 ou
ou 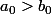
ou faut-il imposer la condition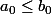 pour assurer la convergence?
pour assurer la convergence?
ou faut-il imposer la condition
- 11 Déc 2021, 13:42
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
On a 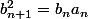 , donc
, donc 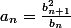 et par suite si les deux suites convergent, elles ont la même limite.
et par suite si les deux suites convergent, elles ont la même limite.
- 11 Déc 2021, 13:38
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
Pour les suites que j'ai donné, ce n'est pas le cas.
Si elles convergent, nécessairement elles ont la
même limite.
Si elles convergent, nécessairement elles ont la
même limite.
- 11 Déc 2021, 12:01
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
J'ai pas bien saisi vos réponses. A-t-on la convergence des suites peu n'importe 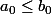 ou
ou 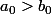 ?
?
@catamat, je ne suis pas d'accord avec vous, si on a la convergence, alors on a l'égalité de deux limites.
@catamat, je ne suis pas d'accord avec vous, si on a la convergence, alors on a l'égalité de deux limites.
- 11 Déc 2021, 10:55
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: comparaison de deux suites
D'accord. On peut montrer que a_{n+1}\leq b_{n+1},\;\;\forall \;n\in\mathbb{N} . De cette inégalité, on peut montrer aussi que : a_n\leq a_{n+1}\leq b_{n+1}\leq b_n,\;\forall\;n\in \mathbb{N}^* Est-ce-qu'on peut déduire que les suites (a_n) et (b_n) sont convergentes? L’inégalité ci-...
- 11 Déc 2021, 07:26
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
comparaison de deux suites
Bonsoir,
J'ai les suites suivantes définies par:
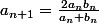 et
et 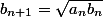 .
.
Supposons que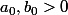 . A-t-on
. A-t-on 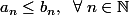 ?
?
Cordialement,
Sylvain.
J'ai les suites suivantes définies par:
Supposons que
Cordialement,
Sylvain.
- 10 Déc 2021, 21:22
- Forum: ✯✎ Supérieur
- Sujet: comparaison de deux suites
- Réponses: 17
- Vues: 681
Re: Analyse complexe
Bonsoir,
S'il vous plait, j'ai besoin de votre aide.
Peut-on appliquer le principe de maximum pour la question 5-b)?
Merci bien d'avance.
S'il vous plait, j'ai besoin de votre aide.
Peut-on appliquer le principe de maximum pour la question 5-b)?
Merci bien d'avance.
- 04 Déc 2021, 16:32
- Forum: ✯✎ Supérieur
- Sujet: Analyse complexe
- Réponses: 3
- Vues: 338
Re: Analyse complexe
J'ai réglé le problème.
- 03 Déc 2021, 14:31
- Forum: ✯✎ Supérieur
- Sujet: Analyse complexe
- Réponses: 3
- Vues: 338
Analyse complexe
Bonjour, J'ai un exercice d'analyse complexe (voir ci-attaché). https://www.cjoint.com/c/KLdnkBz6Pk6 Voici mes réponses: 1- si k=1 , alors f(z)=f(z), donc S_1 est l'ensemble des fonctions holomorphes sur le disque D(0, R). 2- On a f(0)= f(0)^k , donc \vert f(0)\vert =\vert f&...
- 03 Déc 2021, 14:02
- Forum: ✯✎ Supérieur
- Sujet: Analyse complexe
- Réponses: 3
- Vues: 338
- 11 Oct 2019, 19:51
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel
- Réponses: 4
- Vues: 366
Re: Calcul différentiel
C'est ce que j'ai fait mais bizarre l'image n’apparaît pas !!!
- 11 Oct 2019, 19:48
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel
- Réponses: 4
- Vues: 366
Re: Calcul différentiel
L'image n’apparaît pas ici? non?
Sinon, que dois-je faire? J'ai fait " Ajouter des fichiers joints", mais je sais quel est le problème????
Sinon, que dois-je faire? J'ai fait " Ajouter des fichiers joints", mais je sais quel est le problème????
- 11 Oct 2019, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel
- Réponses: 4
- Vues: 366
Calcul différentiel
Bonsoir, J'ai un petit exercice qui m’embête (svp voir l'image ci-attachée). 1) pour la première partie de la 1ère question, je pense qu'on utilise le théorème des fonctions implicites. Pour la 2ème partie, comment définit-on la tangente à la courbe ici tout d'abord? et après pourquoi cette tangente...
- 11 Oct 2019, 18:25
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel
- Réponses: 4
- Vues: 366
Re: Résolvante compacte
Bonjour,
Ok je suis d'accord, juste une petite correction c'est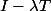 au lieu de
au lieu de 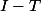 .
.
Merci beaucoup.
Ok je suis d'accord, juste une petite correction c'est
Merci beaucoup.
- 19 Mar 2018, 07:09
- Forum: ✯✎ Supérieur
- Sujet: Résolvante compacte
- Réponses: 7
- Vues: 729
Re: Résolvante compacte
Rebonjour Non tu ne te trompes pas. Mais si T=B^{-1} est borné pour la topologie de H, il l'est aussi pour la topologie de D(A). En effet ||Tu||_{D(A)}=||u||_H+||Tu||_H\leq ||u||_H+c||u||_H =(c+1)||u||_H Excusez moi aviateur, mais c'est pas ça la norme de ||Tu||_{D(A)} . Ce ...
- 18 Mar 2018, 17:20
- Forum: ✯✎ Supérieur
- Sujet: Résolvante compacte
- Réponses: 7
- Vues: 729
Re: Résolvante compacte
Merci très bien aviateur.
- 18 Mar 2018, 16:58
- Forum: ✯✎ Supérieur
- Sujet: Résolvante compacte
- Réponses: 7
- Vues: 729
Re: Résolvante compacte
Merci bien pour votre réponse. Pourquoi B^{-1} est un opérateur borné de H vers D(A) ? Je pense qu'il est borné de H dans H . Me trompe-je? Pour montrer que B^{-1} es compact, on doit montrer l'existence d'une sous suite de (B^{-1} x_n) qui converge dans D(A) ou dans H ?
- 18 Mar 2018, 12:26
- Forum: ✯✎ Supérieur
- Sujet: Résolvante compacte
- Réponses: 7
- Vues: 729
- 25 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
