Forum de Mathématiques: Maths-Forum

Bonsoir,

A tout nombre complexe z différent de -(1+i) on associe le nombre

z' = [iz² - (1-i)z] / (|z+i|² + zbarre - i) .

Montrer que z' = iz\(zbarre - i)

Alors j'ai eu l'idée d'écrire |z + i|² = (z+i)(zbarre-i) mais cela n'aboutit à rien.

Merci d'avance.

Ah c'est beaucoup plus clair maintenant, merci!

Salut Titine, ça devrait faire l'affaire?

Soit A le point d'affixe 1 et f l'application qui à tout point M d'affixe z différent de 1, associe le point N d'affixe f(z) = z/(z-1)

1) a/ Calculer (z-1)(f(z)-1) (Déjà fait, on trouve 1)

b/ En déduire que les demi-droites [AM) et [AN) sont symétriques par rapport à la droite D: y=0.

Salut Razes, cette formule s'applique uniquement pour le centre de gravité d'un triangle.

Bonjour,

http://img4.hostingpics.net/pics/477971cats.jpg

Merci d'avance.

Razes a écrit: Simplifie, Que peux tu constater?

Salut Razes, merci pour ta réponse mais pourquoi remplacer U2n sous la racine par[2-√(U2n-1)]²

Bonsoir,

(Un): U0=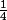 et Un+1=f(Un).

f(x)= (2-)²

J'ai du mal à calculer U2n et U2n+1.

Merci d'avance

Ah, ça m'a échappé.
Merci beaucoup

Bonsoir,
j'ai du mal à calculer cette limite: Limite en 0+ de sin(x).f(1/(sin⁡(x)).
En sachant que f(x)= (2-√x)²
J'ai effectué un changement de variable en posant X=1/sin(x) mais l'indétermination ne se lève pas.
Merci d'avance.