Forum de Mathématiques: Maths-Forum

Salut à tous, la question est celle-ci, j'ai essayé de m'inspirer de la démonstration de la racine de 2 mais ça n'a pas marché. Montrer que \frac{\ln 3}{\ln 2} est irrationnel? merci beaucoup bonjour je pense que le fait de s'inspirer du cas de \sqrt2 veut dire que le début de la démonstration par ...

Bonjour
on peut montrer que pour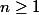
peut -on(savoir) conjecturer le nombre de termes impairs entre ?

v_{n+1}=\frac{1}{4}\left (v_n^2+4v_n-1 \right ) On peuT poser w_n=av_n+b et chercher a et b afin que w_{n+1}=\frac{1}{4}w_n^2 mais ceci n'a pas de solution, le seule format possible est \left (v_{n+1}+1 \right )=\frac{1}{4}\left (v_{n}+1 \right )^2-1 Bonjour plutôt \left ...

bonjour pour un texte plus lisible! comme je l'ai déjà dit au début , la question de parité est venue au cours de l'étude d'une suite que j'ai proposé et que je l'appellerai par la suite suite de digischool1(dS1)qui est : u_0=3, u_{n+1}= u_{n} +"Somme des nombres impairs \leq{u_{n}} ;pour n en...

bonjour pour un texte plus lisible! comme je l'ai déjà dit au début , la question de parité est venue au cours de l'étude d'une suite que j'ai proposé et que je l'appellerai par la suite suite de digischool1(dS1)qui est : u_0=3, u_{n+1}= u_{n} +"Somme des nombres impairs \leq{u_{n}} ;pour n ent...

bonjour
effectivement ,l'astuce "20" donne bien le résultat.
merci.

je vous remercie pour votre réponse .Je vous demande excuse si j'abuse un peu de votre
temps .
j'ai essayé comme vous l'avez signalé mais ça bloque
u(n)=2k+1 ..........> u(n+1) = (k+1)^2+1 dont la parité reste à démontrer!
peut etre j'ai mal vu !

merci beaucoup pour votre indulgence et votre patience . C'est la première fois que je participe
à un forum.
j'ai utilisé la démonstration par récurrence mais je bloque devant
u(n)= 2k+1 ............u(n+1)=(k+1)^2+1 impair ? comment ?

Bonjour en étudiant la suite récurrente suivante : U(0)=3 u(n+1)=(1/4)[(u(n))^2+6u(n)+1] pour n entier naturel je me suis bloqué devant le fait de montrer que : tous les termes de cette suite sont des nombres impairs se terminant par 3 ou par 7? cette suite n'est pas parvenue par hasard mais suite à...