Exercice nombres irrationnels

[ilyassabarbach]

Salut à tous, la question est celle-ci, j'ai essayé de m'inspirer de la démonstration de la racine de 2 mais ça n'a pas marché.
Montrer que est irrationnel?

merci beaucoup

[aymanemaysae]

Bonjour;

supposez d'abord que est rationnel, càd avec et car ,

donc .

Vous pouvez maintenant conclure.

[rassan]

Salut à tous, la question est celle-ci, j'ai essayé de m'inspirer de la démonstration de la racine de 2 mais ça n'a pas marché.
Montrer que est irrationnel?

merci beaucoup

bonjour
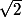
je pense que le fait de s'inspirer du cas de veut dire que le début de la démonstration par l'absurde est connue.
J'ajoute :
passe de ln au puissance et trouve la contradiction en utilisant la parité!

[aymanemaysae]

Bonjour,

le même topic a été discuté sur un autre forum, et la démarche suivie est similaire à la notre.

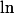
car la fonction est bijective,

et comme a et b sont non nuls et un nombre pair ne peut être égal à un nombre pair, d’où la contradiction,

donc n'est pas un nombre rationnel, donc irrationnel.

[ilyassabarbach]

merciii à vouus infiniment