Forum de Mathématiques: Maths-Forum

Comment justifier que AS=OV ?

Pour exprimer SV en fonction de xs et zs, j'ai d'abord utiliser pythagore puisque SVT est rectangle en T : SV² = VT² + ST² SV² = (xT-xV)² + (yT-yV)² + (zT-zV)² + (xT-xS)² + (yT-yS)² + (zT-zS)² ...... SV² = 100 + xs² + zs² - 10xs + yV² - 10yV Pour remplacer yV² j'ai utilisé AS=OV ce qui m'a donné : x...

Voici l'énoncé de mon DM : Dans un repère orthonormé de l'espace (O,i,j,k), on considère les points A(10;0;0), B (0;10;0) et C (0;0;10). Soit T le milieu du segment [AB]. S un point mobile sur le segment [AC]. On appelle (P) le plan perpendiculaire à la droite (ST) et qui passe par le point T Ce pla...

Merci ! ^^

Je cherche tout simplement la primitive de la fonction suivante :

f(x) =

Malgré avoir mes leçons sur les primitives et l'intégration sous les yeux, je n'y arrive pas... Quelqu'un pour m'éclairer ?

Je ne comprends pas en quoi a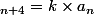 équivaut à dire que n est un multiple de 4, pouvez-vous m'expliquer ?

Merci !

⋅  \left|z \right|= \frac{\sqrt{2}}{2} ⋅  \theta =\frac{-\pi }{4} ⋅  z=\frac{\sqrt{2}}{2}\times e^{i\frac{-\pi }{4}} ⋅  Donc : 4\times (\frac{1}{2}-\frac{1}{2}i)^{n} = 4\times \frac{\sqrt{2}}{2}^{n}\times e^{in\frac{-\pi }{4}} Comment trouver les coor...

Je sais bien mais je ne vois pas où sont a et b ?

Bonjour à tous, voici un DM que j'ai à rendre pour la rentrée (dans deux jours), et je bloque à une question : je connais la réponse mais je doute de sa démonstration... Voici l'énoncé : Le plan complexe est muni d'un repère orthonormal direct (O;u;v). Pour n \in N, on crée la suite de points du pla...

⋅  \left|z \right|= \frac{\sqrt{2}}{2} ⋅  \theta =\frac{-\pi }{4} ⋅  z=\frac{\sqrt{2}}{2}\times e^{i\frac{-\pi }{4}} ⋅  Donc : 4\times (\frac{1}{2}-\frac{1}{2}i)^{n} = 4\times \frac{\sqrt{2}}{2}^{n}\times e^{in\frac{-\pi }{4}} Comment trouver les coor...

Nous n'avons pas encore vu cette formule ! Que représente ? Et que faire du 4 ?

Merci de votre aide.

J'ai l'argument et le module, mais je ne vois pas comment ils pourraient m'aider ?

L'expression exacte est : 4(-i)^n

Bonsoir,

Je cherche en vain à déterminer les coordonnées d'un vecteur d'affixe z= x

Quelqu'un pour m'aider ?

0

En corrigeant mes erreurs de calculs/d'innantention, je trouve bien :



Merci encore pour votre aide!

Je trouve bie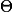n n = n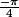, mais je ne comprend pas pourquoi alors que la suite oscille entre

EDIT : J'ai fais une erreur pour les points M3 et plus, merci de votre aide !

Dans ce cas 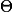3 = -3pi/4

D'accord, mais ce que je ne comprend pas c'est comment calculer l'argument alors qu'il y a une puissance de n... Et surtout comment trouver des arguments sous forme de suite... Tout ce que je sais, en calculant terme par terme, c'est que la fonction \Theta .n a pour premier terme \Theta 0 = 0 et qu'...

Bonjour à tous, je suis en Terminale S, voici un DM que j'ai à faire pour les vacances, je bloque à une question. Le plan complexe est muni d'un repère orthonormal direct (O;u;v). Pour n \in N, on crée la suite de points du plan complexe (M.n) suivante : M0 est le point d'affixe 4 On appele a.n l'af...