Nombres complexes et vecteurs
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 26 Fév 2016, 18:55
par mp33480 » 26 Fév 2016, 18:55
Bonsoir,
Je cherche en vain à déterminer les coordonnées d'un vecteur d'affixe z= x
^{n})
Quelqu'un pour m'aider ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 26 Fév 2016, 19:02
par Manny06 » 26 Fév 2016, 19:02
que représente x ? a et b sont-ils donnés ?
recopie le texte exact pour qu'on puisse t'aider
-
Toutdoux
- Messages: 3
- Enregistré le: 26 Fév 2016, 18:19
-
 par Toutdoux » 26 Fév 2016, 19:07
par Toutdoux » 26 Fév 2016, 19:07
Essaye de passer à l'arg et au module
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 26 Fév 2016, 20:31
par mp33480 » 26 Fév 2016, 20:31
J'ai l'argument et le module, mais je ne vois pas comment ils pourraient m'aider ?
L'expression exacte est : 4

(

-

i)^n
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 27 Fév 2016, 12:14
par Carpate » 27 Fév 2016, 12:14
Tu n'écoutais donc pas quand ton prof. t'a démontré que
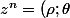^n = (\rho^n;n\theta))
?
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 27 Fév 2016, 13:43
par mp33480 » 27 Fév 2016, 13:43
Nous n'avons pas encore vu cette formule ! Que représente

? Et que faire du 4 ?
Merci de votre aide.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 27 Fév 2016, 15:04
par Pseuda » 27 Fév 2016, 15:04
mp33480 a écrit:J'ai l'argument et le module, mais je ne vois pas comment ils pourraient m'aider ?
L'expression exacte est : 4

(

-

i)^n
Commence par mettre (

-

i) sous forme exponentielle, en calculant d'abord son module, puis en déterminant son argument. Qu'as-tu trouvé ?
Ensuite, tu n'as plus qu'appliquer ce que dit Carpate pour le mettre à la puissance n (regarde ton cours sur les complexes) :
})^n = \rho^n*e^{(in\theta)})
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 27 Fév 2016, 15:25
par mp33480 » 27 Fév 2016, 15:25
Comment trouver les coordonnées du vecteur maintenant ?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 27 Fév 2016, 18:44
par Pseuda » 27 Fév 2016, 18:44
mp33480 a écrit:Comment trouver les coordonnées du vecteur maintenant ?
Eh bien retour à la notation algébrique de ce complexe : a+ib. Les coordonnées du vecteur seront : (a;b).
Ensuite, pour montrer que 2 vecteurs sont colinéaires, il suffit de montrer que leurs coordonnées sont dans un rapport k :

-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 27 Fév 2016, 19:26
par mp33480 » 27 Fév 2016, 19:26
Je sais bien mais je ne vois pas où sont a et b ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 27 Fév 2016, 19:53
par Manny06 » 27 Fév 2016, 19:53
si tu ne veux pas utiliser module et argument cherche les puissances successives de (1-i)
(1-i)²=-2i
(1-i)³=-2-2i
(1-i)^4=-4
ensuite utilise la forme des exposants
si n=4k (1-i)^n=(1-i)^4k=(-4)^k
fais de même si n=4k+1 n=4k+2 n=4k+3
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 28 Fév 2016, 12:36
par mp33480 » 28 Fév 2016, 12:36
PSEUDA a écrit: mp33480 a écrit:Comment trouver les coordonnées du vecteur maintenant ?
Eh bien retour à la notation algébrique de ce complexe : a+ib. Les coordonnées du vecteur seront : (a;b).
Ensuite, pour montrer que 2 vecteurs sont colinéaires, il suffit de montrer que leurs coordonnées sont dans un rapport k :

^{n})
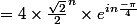
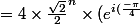})^{n})
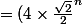(\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2})^{n})
Ensuite je n'y arrive plus, à cause de la puissance.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 28 Fév 2016, 14:43
par Carpate » 28 Fév 2016, 14:43
L'affixe de ton vecteur est donc :
^n[cos(n\frac{\pi}{4})+isin(n\frac{\pi}{4})])
et ses composantes sont :
^n.cos(n\frac{\pi}{4}),4(\frac{\sqrt2}{2})^n.sin(n\frac{\pi}{4})])
-
mp33480
- Membre Naturel
- Messages: 20
- Enregistré le: 24 Fév 2016, 16:03
-
 par mp33480 » 28 Fév 2016, 15:09
par mp33480 » 28 Fév 2016, 15:09
Merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
(
-
i)^n