136 résultats trouvés
Revenir à la recherche avancée
Bonjour !
Je cherche à démontrer qu'une variable aléatoire

à valeurs dans

est d'espérance finie si et seulement si la série
)
converge et que dans ce cas
 = \sum_{k=1}^{\infty} P(X \ge k))
.
Merci d'avance pour votre aide.
- par Kyg
- 05 Mar 2017, 11:21
-
- Forum: ✯✎ Supérieur
- Sujet: Variable à valeurs dans N d'espérance finie
- Réponses: 2
- Vues: 332
On a bien f'(x) = 1/2 * (e^x+e^{-x})-1 - Soit tu utilise une propriété connue du cosinus hyperbolique (=la dérivée du sinus hyperbolique) - Soit... tu dérive une fois de plus pour trouver la propriétés "connue" que... tu ne connais pas... Merci beaucoup, j'ai effective...
- par Kyg
- 03 Déc 2016, 20:36
-
- Forum: ✯✎ Supérieur
- Sujet: Sinus hyperbolique
- Réponses: 36
- Vues: 1404
Justement c'est ça que je n'arrive pas à faire !
On a bien
 = 1/2 * (e^x+e^{-x})-1)
mais je n'arrive absolument pas à trouver le signe de cette expression
- par Kyg
- 03 Déc 2016, 20:14
-
- Forum: ✯✎ Supérieur
- Sujet: Sinus hyperbolique
- Réponses: 36
- Vues: 1404
Bonsoir,
Je n'arrive pas à trouver le signe de la fonction f telle que
 = sh(x)-x)
.
Pourriez-vous m'éclairer ?
Merci.
- par Kyg
- 03 Déc 2016, 19:47
-
- Forum: ✯✎ Supérieur
- Sujet: Sinus hyperbolique
- Réponses: 36
- Vues: 1404
Oui j'avais mal recopié sur l'ordi.
Ok j'ai compris et j'ai rectifié la dimension.
Et là j'ai encore un souci :; il faut en déduire les polynômes

de

qui vérifient
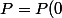+P(1)X+P(2)X^2)
- par Kyg
- 18 Sep 2016, 10:57
-
- Forum: ✯✎ Supérieur
- Sujet: Polynômes interpolateurs de Lagrange
- Réponses: 9
- Vues: 651
Ok merci j'ai trouvé : L_1(X)=\frac{1}{2}X^2-\frac{3}{2}X+1 L_2(X)=-X^2+2X L_3(X)=\frac{1}{2}X^2-\frac{1}{2}X Donc A = \begin{pmatrix} 1 & 0 & 0 \\ -\frac{3}{2} & 2 & -\frac{1}{2} \\ \frac{1}{2} & -1 & \frac{1}{2}\end{pmatrix} J'ai ensuite montré que 1...
- par Kyg
- 18 Sep 2016, 10:10
-
- Forum: ✯✎ Supérieur
- Sujet: Polynômes interpolateurs de Lagrange
- Réponses: 9
- Vues: 651
Ah oui c'était tout bête merci beaucoup !!
Cependant pour la question 3 je ne sais pas.
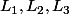
sont des polynômes de degré inférieur ou égal à

Je n'arrive pas à relier les informations entre elles et en effet je ne vois pas trop quelle tête ont ces polynômes.
- par Kyg
- 17 Sep 2016, 16:39
-
- Forum: ✯✎ Supérieur
- Sujet: Polynômes interpolateurs de Lagrange
- Réponses: 9
- Vues: 651
Bonjour, Je bloque sur un exercice sur les polynômes de Lagrange. On a n un entier supérieur ou égal à 3 . On note E = R_{n-1}[X] l’espace vectoriel des polynômes à coefficients réels de degré inférieur ou égal à n-1 et B = (1, X, . . . , X^{n-1}) sa base canonique. On considère n réels a_1,...
- par Kyg
- 17 Sep 2016, 16:17
-
- Forum: ✯✎ Supérieur
- Sujet: Polynômes interpolateurs de Lagrange
- Réponses: 9
- Vues: 651
Bonsoir
Maintenant je dois montrer que
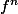
est de classe

sur

et j'avoue que je ne sais pas trop comment m'y prendre..
- par Kyg
- 28 Aoû 2016, 23:08
-
- Forum: ✯✎ Supérieur
- Sujet: Analyse - fonction
- Réponses: 6
- Vues: 401
Merci pour cette réponse, j'ai effectué les mêmes étapes que pour le cas
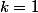
mais je reste bloquée ensuite...
- par Kyg
- 28 Aoû 2016, 13:53
-
- Forum: ✯✎ Supérieur
- Sujet: Application suites réelles
- Réponses: 5
- Vues: 351
Bonsoir, Voilà mon problème : Soit E l'ev des suites réelles. Soit f : E \rightarrow E qui à une suite u associe la suite v avec v_n = u_{n+1} J'ai démontré que f était une application linéaire. J'ai ensuite trouvé que Ker f = Vect((1,0,...,0,...)) et dim(Ker f) = 1 Je dois m...
- par Kyg
- 26 Aoû 2016, 17:42
-
- Forum: ✯✎ Supérieur
- Sujet: Application suites réelles
- Réponses: 5
- Vues: 351
Tu ne réponds pas sur la définition du noyau ? Tu n'as pas de cours sous la main ? Eh bien le noyau de l'application linéaire f de E dans F est l'ensemble {u \in E | f(u) = 0} Donc E_1= {u \in C^2 | (f-z_1id)(u)=0} Mais de là pour trouver la dimension, on peut peut-être util...
- par Kyg
- 17 Aoû 2016, 12:54
-
- Forum: ✯✎ Supérieur
- Sujet: Dimension, base
- Réponses: 9
- Vues: 535
Non je n'ai jamais calculé de base de sous-espaces propres et je ne sais pas ce que signifie réduire un endomorphisme. En fait cet exercice est une initiation aux valeurs propres je suppose, mais c'est la première fois que j'en entends parler et je ne suis pas très à l'aise avec cette notion au nive...
- par Kyg
- 17 Aoû 2016, 10:35
-
- Forum: ✯✎ Supérieur
- Sujet: Dimension, base
- Réponses: 9
- Vues: 535
En fait je ne comprends pas à quoi correspondent

et

et quels systèmes entrent en jeu pour trouver la dimension et la base..
- par Kyg
- 16 Aoû 2016, 21:58
-
- Forum: ✯✎ Supérieur
- Sujet: Dimension, base
- Réponses: 9
- Vues: 535
Bonsoir, J'aurais besoin d'aide pour répondre à la question suivante : Soit la matrice A = \left ( \begin{array}{cc} 1 & i \\ i & 1 \\ \end{array} \right ) \in M_2(C) J'ai trouvé qu'elle admettait z_1 = 1-i et z_2 = 1+i pour valeurs propres dans C . Et maintenant je dois trou...
- par Kyg
- 16 Aoû 2016, 20:17
-
- Forum: ✯✎ Supérieur
- Sujet: Dimension, base
- Réponses: 9
- Vues: 535
Oh mais bien sûr, merci beaucoup de m'avoir débloqué !
Par contre, pourquoi

ne peut pas être négatif ou nul ?

- par Kyg
- 15 Aoû 2016, 21:44
-
- Forum: ✯✎ Supérieur
- Sujet: Analyse - fonction
- Réponses: 6
- Vues: 401
En fait c'est tout bon, j'ai trouvé une démonstration convenable ! Merci beaucoup pour votre aide.
- par Kyg
- 14 Aoû 2016, 23:03
-
- Forum: ✯✎ Supérieur
- Sujet: Surjectivité, injectivité
- Réponses: 9
- Vues: 308
