Forum de Mathématiques: Maths-Forum

Si la période et de: 0,0005s soit O,5 ms et que la base de temps est à: 0,1ms par division La sinusoïde entière fait 5 divisions sur l'axe des "x"; elle passe donc par 0V toutes les 2,5 divisions. Sur l'axe des "y" le haut de la courbe sera à +2,83 divisons et le bas à: -2,83 di...

Je pense avoir compris un peu, sur un des documents que vous m'avez proposé j'ai vu la formule T=base de temps x nv (nombre de divisions verticales en ms) j'ai calculé ainsi pour la question 3)b nv=T/base de temps An nv=0,0005/0,1=0,005ms mais je ne sais toujours pas comment tracer.... Voici les don...

Bonsoir, On m'a donné un exercice et je n'ai pas bien compris une question. Voici l'énoncé: Un générateur délivre une tension sinusoidale de fréquence 2khz et de valeur efficace 2v. 1)Quelle est la tension de crête? 2)Quelle est la période de cette tension? 3)Ce générateur est branché aux plaques de...

Salut ! On cherche a et b tels que, quel que soit x\in\mathbb{R}\setminus \{-2,2\} , on ait ax+2a+bx-2b=1 , ou encore (a+b)x+2a-2b=0x+1 . Or deux polynômes étant égaux si et seulement si leurs coefficients sont égaux, cela équivaut à dire que : [CENTER] \begin{cases} ~ a+b=0 \\ 2a-2b = 1 \e...

Bonsoir j'ai un problème avec cet exercice Déterminer les nombres réels a et b tels que pour tout x élément de IR\(-2;2) on ait: 1/x²-4=a/x-2+b/x+2 J'ai commencé à traiter l'exercice, j'ai réduit au même dénominateur les membres de droite: 1/x²-4=ax+2a+bx-2b/x²-4 j'élimine les dénominateurs ce qui m...

7=3x²-3x+1 0=3x²-3x+1-7 0=3x²-3x-6 3(x²-x-2)=0 x²-x-2=0 :mur: après avoir calculé ça -1 est racine évidente à partir de là on factorise (x+1)(x-2)=0 on obtient x1=-1 et x2=2 maintenant je me demandais comment formuler tout le processus (je dois corriger l'exercice au tableau et expliquer le chemine...

Peut être plus simple: y=1-x x^3+y^3=x^3+(1-x)^3=7 le terme en x^3 disparait après développement et ne reste qu'un facile second degré. Je comprends un peu mieux j'ai remplacé y=1-x et (x+y) par sa valeur 1 puis j'ai développé ça m'a bel est bien donné 7=3x²-3x+1 mais j'ai pas compris que il est pa...

pour la première il suffit de retourner au collège et reconnaître un facteur commun :: 2x^2 - 26x = 2x(x - 13) = 0 ... pour la seconde la somme de deux nombres négatifs -2x^2 -40 dont l'un l'est strictement peut-elle être nulle ? Je suis un peu distrait excuse moi ^^ en effet ça m'aurait év...

salut ou alors x³+y³=(x+y)(x²-xy+y²) 7=x²-xy+y² 7=x²-x(1-x)+(1-x)² 7=3x²-3x+1 x²-x-2=0 (x+1)(x-2)=0 deux solutions: (-1,2) (2,-1) Ce sont des équations et non des inéquations :zen: J'ai corrigé mon erreur dans le titre désolé. Et euh sinon je comprend pas que de (x+y)(x²-xy+y²) tu obtiennes 7=x²-xy...

Bonsoir j'ai un problème avec un système d'équations :


Je ne connais que le genre

où on utilise Somme et Produit pour résoudre

zygomatique a écrit:salut

est-il besoin de calculer le discriminant pour ces deux équations ?

....

Euh comment connaitre les solutions sinon... y'a pas de racine évidente ou bien?

mathelot a écrit:La 1ère équation donne comme solutions
la seconde équation n'a pas de solution.

Ah donc mon travail est correcte merci pour ton aide mais aurais-tu une méthode avec le tableau de signe? c'est souvent ce qu'exige mon prof.

je vous propose de résoudre deux équations , puis de vérifier les solutions car |a|=a ou |a|=-a selon le signe de a. Je n'avais pas bien compris désolé mais j'ai saisi le truc voici mon cheminement pour 1) soit 2x²-13x+20=13x +20 je transpose les membres et ça donne 2x²-26x=0 et je résous ;)=676 x1...

mathelot a écrit:résout les deux équations





et comme c'est brut de fonderie, on vérifie ensuite que les valeurs trouvées sont solutions
(ou non).

si je comprends bien je dois résoudre chaque membre( et ) séparemment?

Bonjour j'ai un problème avec l'équation suivante:
Résoudre dans IR les équations suivantes

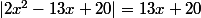
Enfait j'ai un problème pour les valeurs absolues en général...

Bonsoir Eh bien, il faut résoudre ce système graphiquement . Donc soit tu as un graphique déjà tracé et tu essaies de trouver les solutions, soit tu dois traces le graphique à l'aide de la deuxième indication : x+y=1. J'ai pas le graphique. J'ai tracé le graphique x+y=1 mais que dois-je faire de l'...

Bonsoir j'ai un peu de mal sur un exercice. Voila : On dis : \text{Resoudre graphiquement le systeme suivant}: \left\{ \begin{array} |x-1|\leq 1 \\ x+y=1 \end{array} \right. Je n'ai jamais eu à faire à ce genre de système donc je ne sais pas si je dois résoudre l'équation et l'inéquation dans le rep...

Sake a écrit:Ah non j'en doute !

Hum j'avais oublié le donc ça va me donner

\fra{1}{1\times 2}+\fra{1}{2\times 3}+\fra{1}{3\times 4}+\ ...\ \ =(\fra{1}{1}-\fra{1}{2})+(\fra{1}{2}-\fra{1}{3})+(\fra{1}{3}-\fra{1}{4})+\ ...\ =\fra{1}{1}-\fra{1}{2}+\fra{1}{2}-\fra{1}{3}+\fra{1}{3}-\fra{1}{4}+\ ...\ AH d'accord là je vois bien on peut en déduire que \fra...

Salut Tu pars de l'expression de droite et tu la transformes en réduisant au même dénominateur. Tu obtiens l'expression de gauche donc tu as l'égalité. Ensuite \fra{1}{1\times 2}+\fra{1}{2\times 3}+\fra{1}{3\times 4}+\ ...\ \ =\fra{1}{1}-\fra{1}{2}+\fra{1}{2}-\fra{1}{3}+\fra{1}{3}-\fra{1}{4}+\ ...\...