Forum de Mathématiques: Maths-Forum

On demande de montrer que tan(9°)-tan(27°)-tan(63°)+tan(81°)=4

J'ai essayé avec tan(kx) k=3, 4, 9 mais je n'aboutis pas.

Merci pour toute suggestion

zygomatique a écrit:salut

il suffit de considérer la fonction ....

cette fonction est strictement décroissante comme somme de deux fonctions strictement décroissantes ...

Merci infiniment!!!

WillyCagnes a écrit:bsr

si x=1
on a 2+3=5>4

si x=2
2²+3²=13< 4²

x est compris entre 1 et 2
soit 1,50713...

Merci WillyCagnes.
Le plus dur c'est l'unicité!!
Tu as une idée?

Bonjour,
je bloque dans le problème suivant:

Démontrez que n'admet qu'une seule solution reelle.


merci a tous.

chan79 a écrit:Il y a une formule : 1+E((ln(2*pi)-2n+ln(n)*(1+2n))/(2*ln(10)))

pour n=100, elle donne 158

C'est bien ceci:

Est-ce possible de s'y prendre algébriquement?

Salut
Ma question est trés simple:
Combien y a-t-il de chiffres dans 100! ?

Merci

kiminoou a écrit:oui c'est sa sauf que ce n'est pas x tend vers -pie/2 mais x tend vers -pie/4
désolée je suis nouvelle j'ai un peu de mal avec les écritures ..

Dans ce cas il n'y a pas d'indétérmination!!!

Bon voila je vous expose mon problème j'ai eu plusieurs limites en trigonométrie a faire j'ai reussie à les faire tous sauf un qui me pose définitivement problème et que je n'arrive pas à regler le voici : lim -pie/4 ( 2x/tanx+1) des idées ? Merci d'avance Tu veux dire \lim_{x\to -\frac{\pi}{2}}\fr...

zygomatique a écrit:salut

peut-être serait-il plus judicieux d'utiliser la transformation cos p - cos q = ....

Qu'est ce que ceci peut-il rapporter?
Tu as une idée?
Merci

Salut, j'ai la serie suivante: \sum\limits_{i=1}^{\infty} \frac{ (-1)^{i+1}}{ \left(2i-1\right)^3} \left(\cos \left(\frac{\pi (2i-1)}{2} r_1\right)-\cos \left(\frac{\pi (2i-1)}{2} r_2\right)\right) pour 0\leq r_1<r_2\leq 1 J'ai remplacer le cos...

deltab a écrit:oui, reste à justifier cette égalité.

Tu veux dir qu'il faut voir si la fonction à l'interieur de l'integral est uniformement continue en t?

Bonjour. En calculant F'(t) , 1ère indication de Pythales (par dérivation sous le signe intégral (pas difficile à justifier) en intégrant ensuite par parties , on arrive à un autre problème de Cauchy à savoir \left\lbrace \begin{\array} F'(t)=\dfrac{t}{2}F(t) \\ F...

bonjour je mets t en place de lambda une suggestion: remarque que ton intégrale est la partie réelle de l'intégrale de Exp(-x²+itx) Calcule alors l'intégrale de la fonction holomorphe Exp(-z²) sur le contour du rectangle de sommets: 0 , R , R - iu , -iu (cette intégrale est nulle d'après Cauchy) av...

Bonjour,

On demande de calculer L'intégral sachant que 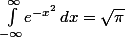pour un .

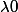Merci pour tte suggestion!!

Kelenner a écrit:Bah personne n'est à l'abri de ce genre de canular... J'espère que mon v(n) fonctionne... Cevas n'a pas l'air de dire qu'il s'en est tiré...

Bien cordialement.

Je m'en suis tiré 2 fois par ton indication et une autre par celle de Ben314.

Merci

Ben314 a écrit:Je me suis "salit les mains", i.e. j'ai calculé les premiers termes à sommer et j'ai commencé à les ajouter pour voir comment ça se goupillais au niveau des simplifications.

Merci

Kelenner a écrit:Dans votre indication plus haut, si on fait $n=1$, j'ai l'impression que l'on trouve 6=1.

Je me trompe ?

Cordialement.

comment tu as pu savoir que c'est une serie téléscope?

Merci

Salut, Indication : 5$\ 6^n=(3^n-2^n)^2-(3^{n+1}-2^{n+1})(3^{n-1}-2^{n-1}) qui est un cas particulier de 5$\ \alpha\beta(a-b)^2-(\alpha a-\beta b)(\beta a-\alpha b)=(\alpha-\beta)^2 ab L'indication et trés éfficace, comment l'a tu vu. il y a q...

Je dois calculer la valeur de cette serie numerique:


Je crois qu'on peut reduire le tout en une serie géométrique, mais je n'y parviens pas!!

Merci d'avance!!

Ben314: Je crois que la procedure est la même que quand on demande la surface entre deux courbes (y=x² et y= -x² +3). On va determiner d'abord l'intersection entre les deux courbes (on trouve deux points mais ne va pas dire il n y a pas de surface entre deux points) et aprés on passe à l'integrale. ...