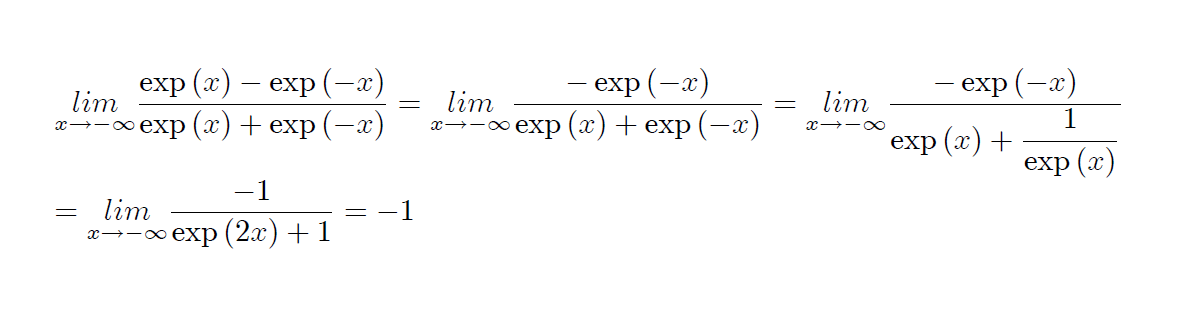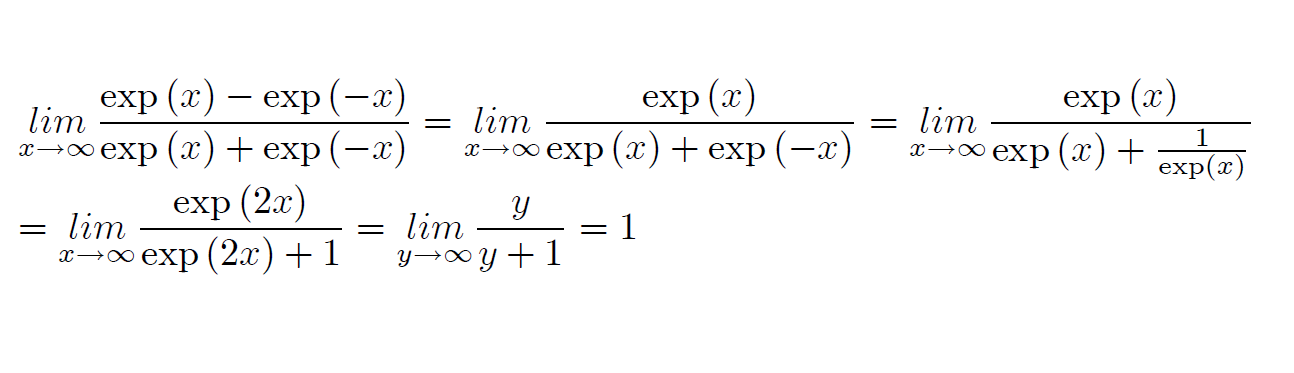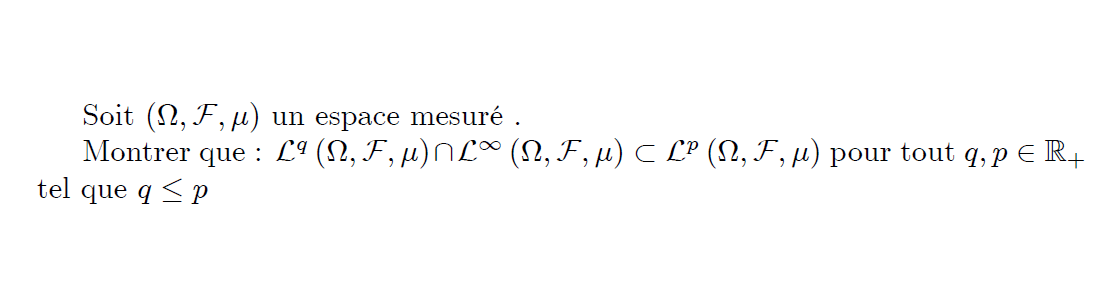
42 résultats trouvés
Revenir à la recherche avancée
- 23 Déc 2016, 15:11
- Forum: ✯✎ Supérieur
- Sujet: Les espaces Lp
- Réponses: 1
- Vues: 191
- 16 Déc 2016, 00:01
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
Re: L'inégalité de Wirtinger.
\int_{S_1}|g(\theta)|^2d\theta=2\pi\sum_{k\in{\mathbb Z}}|\widehat{g}(k)|^2 \int_{S_1}|g'(\theta)|^2d\theta=2\pi\sum_{k\in{\mathbb Z}}|\widehat{g'}(k)|^2=2\pi\sum_{k\in{\mathbb Z}}|ik\widehat{g}(k)|^2 Pourquoi la première somme est-elle forcément plus...
- 15 Déc 2016, 14:43
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
Re: L'inégalité de Wirtinger.
\int_{S_1}|g(\theta)|^2d\theta=2\pi\sum_{k\in{\mathbb Z}}|\widehat{g}(k)|^2 \int_{S_1}|g'(\theta)|^2d\theta=2\pi\sum_{k\in{\mathbb Z}}|\widehat{g'}(k)|^2=2\pi\sum_{k\in{\mathbb Z}}|ik\widehat{g}(k)|^2 Pourquoi la première somme est-elle forcément plus...
- 15 Déc 2016, 14:18
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
Re: L'inégalité de Wirtinger.
Ben314 a écrit:Avec ça et les relations de Plancherel, c'est fini.
Comment ?
- 15 Déc 2016, 00:50
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
Re: L'inégalité de Wirtinger.
Tu n'as évidement pas à "calculer" ces intégrales (comment voudrait tu le faire sans plus d'info. sur f ?) Ce que tu as à faire, c'est le lien entre les intégrales définissant les \widehat g(k) et celle définissant les \widehat{g'}(k) de façon à trouver le lien entre l...
- 14 Déc 2016, 21:05
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
- 14 Déc 2016, 14:17
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
- 14 Déc 2016, 14:00
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
Re: L'inégalité de Wirtinger.
C'est défficile
- 14 Déc 2016, 00:00
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
- 13 Déc 2016, 17:48
- Forum: ✯✎ Supérieur
- Sujet: L'inégalité de Wirtinger.
- Réponses: 13
- Vues: 1249
- 10 Déc 2016, 17:10
- Forum: ✯✎ Supérieur
- Sujet: L'espace W(B(0,1))^1,p
- Réponses: 5
- Vues: 377
Re: L'espace W(B(0,1))^1,p
Doit prouver l'appartenance de  de
de ) et trouver les conditions sur
et trouver les conditions sur  et
et  .
.
- 10 Déc 2016, 17:00
- Forum: ✯✎ Supérieur
- Sujet: L'espace W(B(0,1))^1,p
- Réponses: 5
- Vues: 377
Re: L'espace W(B(0,1))^1,p
Je ne savais pas comment trouver les conditions pour lesquelles  est dans
est dans )
- 10 Déc 2016, 16:12
- Forum: ✯✎ Supérieur
- Sujet: L'espace W(B(0,1))^1,p
- Réponses: 5
- Vues: 377
L'espace W(B(0,1))^1,p
Salut Je ne savais pas comment prouver que u est dans L^{P}(\Omega ) Soit, dans l'espace \mathbb{R}^{N} ,la boule unité ouverte \Omega =B(0,1) . On pose : r^{2}=\sum_{i=1}^{N}x_{i}^{2} . Soit u défi
nie par : u(x)=(1-r )^{\beta }(-ln(1-r))^{\alpha } o...
- 10 Déc 2016, 12:26
- Forum: ✯✎ Supérieur
- Sujet: L'espace W(B(0,1))^1,p
- Réponses: 5
- Vues: 377
Re: Devoir sur sommes et produits
\frac{\exp^x-exp^-^x }{exp^x+exp^-^x} Excusez moi encore de vous déranger mais j'aimerais savoir comment trouver les limites en -infini et +infini car je sais que les limites sont -1 et 1 mais Jai beau leve l'indetermination Jai quand même du mal à sortir de la forme indéterminée http://www12.0zz0....
- 09 Déc 2016, 23:19
- Forum: ✯✎ Supérieur
- Sujet: Devoir sur sommes et produits
- Réponses: 22
- Vues: 1273
- 09 Déc 2016, 23:16
- Forum: ✯✎ Supérieur
- Sujet: Limite exponentielle forme indéterminée
- Réponses: 7
- Vues: 1180
- 09 Déc 2016, 23:00
- Forum: ✯✎ Supérieur
- Sujet: Limite exponentielle forme indéterminée
- Réponses: 7
- Vues: 1180
Re: Limite exponentielle forme indéterminée
x tends vers qulle valeure ?
- 09 Déc 2016, 22:40
- Forum: ✯✎ Supérieur
- Sujet: Limite exponentielle forme indéterminée
- Réponses: 7
- Vues: 1180
Inégalité
Démontrer l'inégalité suivante : \forall \varphi \in D\left ( \mathbb{R}^{n} \right ) , \forall i=1,..n : \left \| \frac{\partial \varphi }{\partial x_{i}} \right \|_{L^{2}\left ( \mathbb{R}^{n} \right )}\leq \left \| \varphi \right \|_{L^{2}\left ( \mathbb{R}^{n} \right )}\l...
- 15 Aoû 2016, 17:41
- Forum: ✯✎ Supérieur
- Sujet: Inégalité
- Réponses: 2
- Vues: 276
- 26 Mai 2016, 02:21
- Forum: ✯✎ Supérieur
- Sujet: inverse continue de Banach
- Réponses: 1
- Vues: 320
- 42 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :