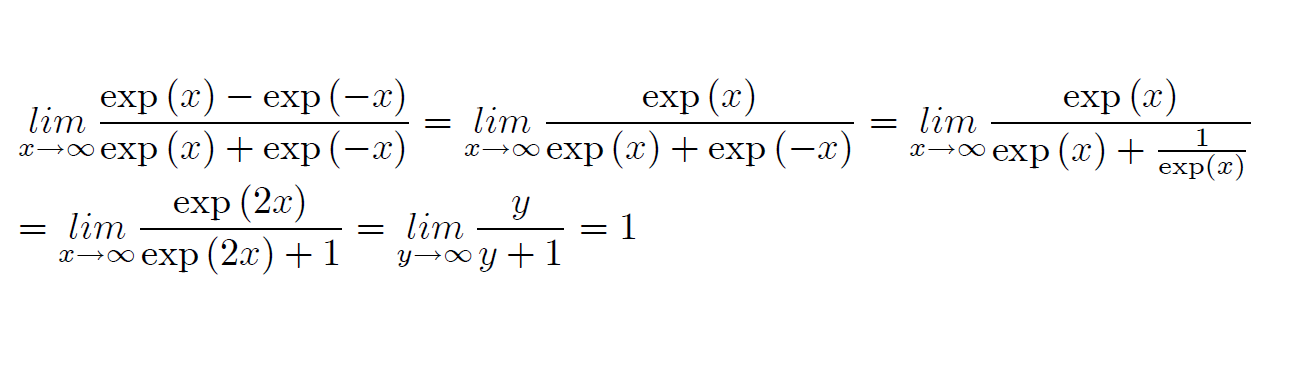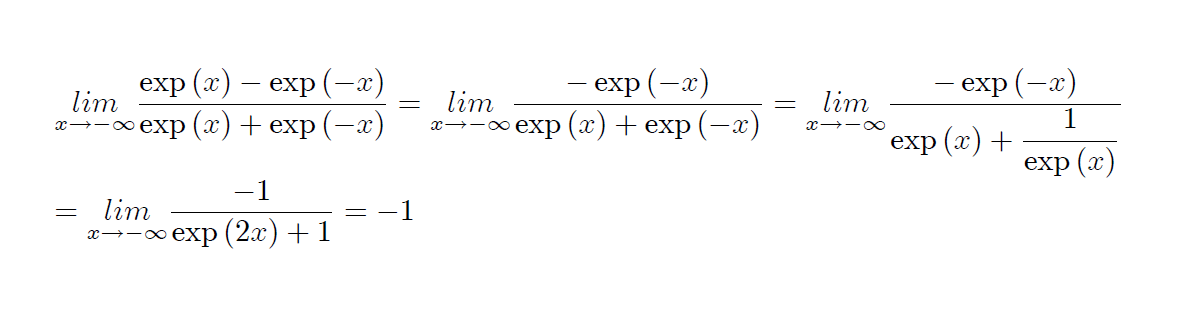Devoir sur sommes et produits

[Amel]

bonjour, Jai jn devoir maison à rendre et j'aurais besoin d'aide qqn saurait-il faire ce genre de démonstration par récurence ?

[Pseuda]

Bonsoir,

Je te suggère d'expliciter les formules avec des .... . Cela permet d'y voir beaucoup plus clair. Ensuite, la récurrence sur n est très facile.

[Sake]

Salut,

Il faut, pour montrer cette égalité pour tout n et pour tout p, démontrer l'égalité pour tout n en fixant p, et pour tout p en fixant n. Il s'agit donc dans le plus long des cas d'une démonstration en deux récurrences.

Comme l'a dit Pseuda, la récurrence sur n est aisée et je vais la poster ici pour mettre la machine en branle.
Reviens vers nous pour d'autres problèmes.

http://img11.hostingpics.net/pics/92052520161209222056.jpg

[Amel]

Je vous remercie pour vos réponses et pour votre grand aide ! je comprend bien mieux à présent !!

[Amel]

Excusez moi encore de vous déranger mais j'aimerais savoir comment trouver les limites en -infini et +infini car je sais que les limites sont -1 et 1 mais Jai beau leve l'indetermination Jai quand même du mal à sortir de la forme indéterminée

[Sake]

Si ce sujet ne concerne pas, de près ou de loin, l'exercice d'avant, nous t'invitons à ouvrir un autre sujet afin de garder une certaine cohérence vis à vis du thème traité. Merci.

[Amel]

c'était sur le meme devoir mais dans Ce cas j'ouvre un nouveau sujet

[Sake]

Pour répondre un tant soit peu à ta question néanmoins, il vient à l'esprit que le comportement en l'infini est mis en exergue si l'on réussit à faire apparaître, dans la formule, des termes qui sont très petits devant d'autres à la fois au numérateur et au dénominateur.

Une bonne façon de procéder est de factoriser par exp(x) pour une étude asymptotique en plus l'infini, et par exp(-x) en moins l'infini.

PS : Merci pour l'effort, je vais demander à un modérateur de transférer les derniers messages dans le sujet que tu créeras.

[Amel]

je vous remercie j'ai ouvert un forum sur le sujet
Jai essayé de factoriser par e^x je vais essayer de faire selon ce que vous m'avez dit
merci

[Sake]

On continue sur l'autre sujet.

[Amel]

J'aurais une question sur la récurence qui A ete envoyé à la fin il y a n+p+2 et je n'ai pas compris vraiment comment on a obtenu ce résultat ?

[Ben314]

Il faut, pour montrer cette égalité pour tout n et pour tout p, démontrer l'égalité pour tout n en fixant p, et pour tout p en fixant n. Il s'agit donc dans le plus long des cas (???) d'une démonstration en deux récurrences.

Euhhhhh.
Je suis pas franchement d'accord (du tout...).
Si tu as montré que :
Quelque soit p, puis quelque soit n, on a . . .
C'est heureusement pas la peine de montrer ensuite que
Quelque soit n, puis quelque soit p, on a . . .
Les quantificateurs "de même nature", ils commutent entre eux :
Écrire
c'est totalement la même chose que

Bref, dans un cas pareil, il suffit de faire une récurrence sur n OU BIEN une récurrence sur p (ou bien... autre chose).

[Sake]

Cela provient d'une manipulation sur le produit des n + j :

à n donné,

[Sake]

C'est vrai.

[Amel]

J'ai un peu de mal à comprendre mais je pense avoir cerné le principal merci à vous.

[algharib]

Excusez moi encore de vous déranger mais j'aimerais savoir comment trouver les limites en -infini et +infini car je sais que les limites sont -1 et 1 mais Jai beau leve l'indetermination Jai quand même du mal à sortir de la forme indéterminée

[Amel]

je vous remercie

[zygomatique]

salut

pour tout p :



donc



donc la propriété est héréditaire ... en fonction de n ...

[Ben314]

Tant qu'à faire d'utiliser des factorielles, on peut même continuer dans la foulée et utiliser des coefficients binomiaux :
Pour tout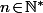 et ,

Ce qui correspond à la somme des termes d'un "morceau" de colonne sur le triangle de pascal et c'est connu comme le loup blanc que ça vaut le coeff. binomial "en dessous à droite" du terme du bas de la colonne (la preuve par récurrence se fait de tête en utilisant la formule additive qui permet de construire le triangle de pascal).
Donc

[Amel]

Merci de votre aide