Bonjour,
On donne la suite (Un):
U(n+1)=(Un +2)/3 et Uo=2
1) Déterminer les quatre premiers termes.
2) Démontrer que (Un) est décroissantes.
1) Uo=2
U1=4/3
U2=5/3
U3=11/9
2) U(n+1)-Un=2/3*(1-Un) là je suis bloqué
U(n+1)/Un=(Un +2)/(3*Un) là aussi je suis bloqué.
Merci d'avance.
Suite récurrente
Règles du forum
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
9 messages
- Page 1 sur 1
Re: Suite récurrente
Bonjour,
U1 OK
U2 je pense qu'il y a une erreur de calcul
U3 OK
Pour la décroissance, étudiez la fonction f(x)= (x+2)/3
U1 OK
U2 je pense qu'il y a une erreur de calcul
U3 OK
Pour la décroissance, étudiez la fonction f(x)= (x+2)/3
Re: Suite récurrente
Oui, U2=10/9
f(x)= (x+2)/3=1/3*x+2/3
f est affine, coefficient directeur positif donc f croissante.
J'ai l'impression que c'est le contraire de ce que je dois démontrer.
A moins que j'oublie des choses.
f(x)= (x+2)/3=1/3*x+2/3
f est affine, coefficient directeur positif donc f croissante.
J'ai l'impression que c'est le contraire de ce que je dois démontrer.
A moins que j'oublie des choses.
Re: Suite récurrente
Bonjour
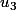 est faux également
est faux également
ensuite, attention, ce n'est pas parce que f sera croissante ou décroissante que la suite sera croissante ou décroissante
ce raisonnement est faux (ce raisonnement est à utiliser si tu as une suite du type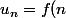) ce qui n'est pas le cas ici )
ce qui n'est pas le cas ici )
tu peux évaluer et tu verras que le simple fait de savoir comparer
et tu verras que le simple fait de savoir comparer  à 1te permettra de répondre
à 1te permettra de répondre
il suffit de montrer par une petite récurrence que tous les termes de ta suite sont supérieurs à 1.
ensuite, attention, ce n'est pas parce que f sera croissante ou décroissante que la suite sera croissante ou décroissante
ce raisonnement est faux (ce raisonnement est à utiliser si tu as une suite du type
tu peux évaluer
il suffit de montrer par une petite récurrence que tous les termes de ta suite sont supérieurs à 1.
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Suite récurrente
une autre solution encore plus simple
tu fais une petite récurrence pour montrer directement que la suite est décroissante (en utilisant le fait que f elle est une fonction croissante)
l'hérédité est très facile
soit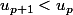 alors ...les images par f ....
alors ...les images par f ....
tu fais une petite récurrence pour montrer directement que la suite est décroissante (en utilisant le fait que f elle est une fonction croissante)
l'hérédité est très facile
soit
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Suite récurrente
f croissante.
Uo=2
f(2)=4/3
f(4/3)=10/9
f(10/9)=28/27
Il semble que (Un) est décroissante.
Supposons que (Un) est décroissant au rang n, U(n+1)<=Un
f(U(n+1))<=f(Un) car f croissante
Donc U(n+2)<=U(n+1)
donc (Un) est décroissante.
(je n'ai pas tout rédigé).
Si c'est bon, je passerai au reste: (Un) est minorée comme tu l'as remarqué.
Uo=2
f(2)=4/3
f(4/3)=10/9
f(10/9)=28/27
Il semble que (Un) est décroissante.
Supposons que (Un) est décroissant au rang n, U(n+1)<=Un
f(U(n+1))<=f(Un) car f croissante
Donc U(n+2)<=U(n+1)
donc (Un) est décroissante.
(je n'ai pas tout rédigé).
Si c'est bon, je passerai au reste: (Un) est minorée comme tu l'as remarqué.
Re: Suite récurrente
oui, tu n'oublieras pas d'initialiser ta récurrence
mais c'est bien ça
Bonne suite d'exo !
mais c'est bien ça
Bonne suite d'exo !
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Suite récurrente
Voici la suite du sujet
Démontrer que (Un) est convergente et déterminer sa limite.
P(n): Un >=1
Uo=2 donc vrai.
Supposons que P(n) vraie au rang n
f(Un) >= f(1) car f croissante.
U(n+1)>=1, l'hérédité est démontrée.
(Un) décroissante et minorée par 1 donc (Un) est convergente.
Soit L sa limite
L=(L+2)/3
L=1
Démontrer que (Un) est convergente et déterminer sa limite.
P(n): Un >=1
Uo=2 donc vrai.
Supposons que P(n) vraie au rang n
f(Un) >= f(1) car f croissante.
U(n+1)>=1, l'hérédité est démontrée.
(Un) décroissante et minorée par 1 donc (Un) est convergente.
Soit L sa limite
L=(L+2)/3
L=1
Re: Suite récurrente
oui, car f est une fonction continue
OK.
OK.
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
