Exercice dénombrement

[cpS]

Bonjour,

J'ai un exercice à faire sur les dénombrements et le binôme de Newton mais je ne réussi pas à le faire:

Voici l'énoncé:
Soit E un ensemble à n éléments.
1. montrer que l'application Béta définie sur P(E) par Béta: X=> "X barre" est une bijection
2. en déduire le calcul de S= ==> le point d'interrogation étant un "appartient à"
3. Calculer : Sn= ==> n/k étant un coefficient binomial
4. Démontrer grâce aux coefficients binomiaux le 1/c)

Merci pour toute aide apportée

[barbu23]

Bonjour,
Quel est le sens de ? le complémentaire ?
Si, c'est le cas, il suffit de trouver tel que : .
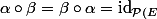Dans ce cas là, est une bijection.
Cordialement. :happy3:

[Sourire_banane]

Bonjour,

J'ai un exercice à faire sur les dénombrements et le binôme de Newton mais je ne réussi pas à le faire:

Voici l'énoncé:
Soit E un ensemble à n éléments.
1. montrer que l'application Béta définie sur P(E) par Béta: X=> "X barre" est une bijection
2. en déduire le calcul de S= ==> le point d'interrogation étant un "appartient à"
3. Calculer : Sn= ==> n/k étant un coefficient binomial
4. Démontrer grâce aux coefficients binomiaux le 1/c)

Merci pour toute aide apportée

Salut,

1) On peut montrer que cette application est injective et surjective (Il existera toujours une partie de E qui sera le complémentaire d'une autre partie en utilisant le fait que (Xbar)bar=X) donc bijective.
2) Il existe une bijection de P(E) dans P(E) donc on peut dénombrer les parties ayant k éléments, k<=n (n=Card(E)). Combien y en a-t-il ?
3) k*(k parmi n)=n(k-1 parmi n-1)
4) Où est le 1)c) ?

[Sourire_banane]

Bonjour,
Quel est le sens de ? le complémentaire ?
Si, c'est le cas, il suffit de trouver tel que : .
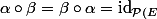Dans ce cas là, est une bijection.
Cordialement. :happy3:

C'est vrai, justement j'y avais pas pensé mais beta est une involution, bien vu ! (et dire que j'ai partiellement utilisé ce fait dans ma méthode ^^)

[cpS]

Salut,

1) On peut montrer que cette application est injective et surjective (Il existera toujours une partie de E qui sera le complémentaire d'une autre partie en utilisant le fait que (Xbar)bar=X) donc bijective.
2) Il existe une bijection de P(E) dans P(E) donc on peut dénombrer les parties ayant k éléments, k<=n (n=Card(E)). Combien y en a-t-il ?
3) k*(k parmi n)=n(k-1 parmi n-1)
4) Où est le 1)c) ?

le 1.c) correspond en fait à la question 3

[Sourire_banane]

le 1.c) correspond en fait à la question 3

J'y ai donc répondu, il reste plus qu'à faire la question 3 X)

En fait, en utilisant le fait que X->Xbar est une bijection, elle admet une bijection réciproque et sommer sur les X (parties de E) revient à sommer sur leurs complémentaires Xbar.
Donc somme des card(X) = somme des card(Xbar)
Alors puisque card(X)+card(Xbar)=card(E)=n, on a somme des card(X)+somme des card(Xbar)=2*somme des card(X)= somme des 2*card(X)=somme des n pour X dans P(E).
Alors somme des card(X)=1/2*somme des n pour X dans P(E)=1/2*n*2^n=n*2^(n-1) puisque E contient 2^n parties.

Cela te permet donc de calculer Sn puisque je te demande toujours de me justifier une autre écriture de la somme du début.

[cpS]

Bonjour,
Quel est le sens de ? le complémentaire ?
Si, c'est le cas, il suffit de trouver tel que : .
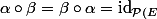Dans ce cas là, est une bijection.
Cordialement. :happy3:

je ne comprend pas bien votre raisonnement avec l'élément identique pouvez-vous m'expliquer s'il vous plait?

[cpS]

J'y ai donc répondu, il reste plus qu'à faire la question 3 X)

En fait, en utilisant le fait que X->Xbar est une bijection, elle admet une bijection réciproque et sommer sur les X (parties de E) revient à sommer sur leurs complémentaires Xbar.
Donc somme des card(X) = somme des card(Xbar)
Alors puisque card(X)+card(Xbar)=card(E)=n, on a somme des card(X)+somme des card(Xbar)=2*somme des card(X)= somme des 2*card(X)=somme des n pour X dans P(E).
Alors somme des card(X)=1/2*somme des n pour X dans P(E)=1/2*n*2^n=n*2^(n-1) puisque E contient 2^n parties.

Cela te permet donc de calculer Sn puisque je te demande toujours de me justifier une autre écriture de la somme du début.

Par rapport à la question 2 et au dénombrement des parties, y-en a-t-il 2^n?

[cpS]

J'y ai donc répondu, il reste plus qu'à faire la question 3 X)

En fait, en utilisant le fait que X->Xbar est une bijection, elle admet une bijection réciproque et sommer sur les X (parties de E) revient à sommer sur leurs complémentaires Xbar.
Donc somme des card(X) = somme des card(Xbar)
Alors puisque card(X)+card(Xbar)=card(E)=n, on a somme des card(X)+somme des card(Xbar)=2*somme des card(X)= somme des 2*card(X)=somme des n pour X dans P(E).
Alors somme des card(X)=1/2*somme des n pour X dans P(E)=1/2*n*2^n=n*2^(n-1) puisque E contient 2^n parties.

Cela te permet donc de calculer Sn puisque je te demande toujours de me justifier une autre écriture de la somme du début.

Est-ce la réponse de 2) ou 3)?
lorsque vous dîtes que c'est égal à la sommes des n pour X dans P(E), voulez-vous dire X parmi n? je ne comprend pas bien la fin de votre raisonnement...

[barbu23]

je ne comprend pas bien votre raisonnement avec l'élément identique pouvez-vous m'expliquer s'il vous plait?

est l'application identité définie par : .
Si tu regardes dans ton cours, tu trouveras la définition suivante :
est bijective

telle que : et

telle que : et

N.B. : Oui, @Sourire_Banane, est une involution. :happy3:
Cordialement. :happy3:

[Sourire_banane]

Est-ce la réponse de 2) ou 3)?
lorsque vous dîtes que c'est égal à la sommes des n pour X dans P(E), voulez-vous dire X parmi n? je ne comprend pas bien la fin de votre raisonnement...

Plutôt de 2 que de 3. Et pour le 3 il n'y a quasiment rien à faire sinon se ramener au cas du 2.

[cpS]

J'y ai donc répondu, il reste plus qu'à faire la question 3 X)

En fait, en utilisant le fait que X->Xbar est une bijection, elle admet une bijection réciproque et sommer sur les X (parties de E) revient à sommer sur leurs complémentaires Xbar.
Donc somme des card(X) = somme des card(Xbar)
Alors puisque card(X)+card(Xbar)=card(E)=n, on a somme des card(X)+somme des card(Xbar)=2*somme des card(X)= somme des 2*card(X)=somme des n pour X dans P(E).
Alors somme des card(X)=1/2*somme des n pour X dans P(E)=1/2*n*2^n=n*2^(n-1) puisque E contient 2^n parties.

Cela te permet donc de calculer Sn puisque je te demande toujours de me justifier une autre écriture de la somme du début.

Lorsque vous marquez "n pour x" c'est une combinaison?

[cpS]

Lorsque vous marquez "n pour x" c'est une combinaison?

La somme du début est-ce que c'est 2^n?

[cpS]

J'y ai donc répondu, il reste plus qu'à faire la question 3 X)

En fait, en utilisant le fait que X->Xbar est une bijection, elle admet une bijection réciproque et sommer sur les X (parties de E) revient à sommer sur leurs complémentaires Xbar.
Donc somme des card(X) = somme des card(Xbar)
Alors puisque card(X)+card(Xbar)=card(E)=n, on a somme des card(X)+somme des card(Xbar)=2*somme des card(X)= somme des 2*card(X)=somme des n pour X dans P(E).
Alors somme des card(X)=1/2*somme des n pour X dans P(E)=1/2*n*2^n=n*2^(n-1) puisque E contient 2^n parties.

Cela te permet donc de calculer Sn puisque je te demande toujours de me justifier une autre écriture de la somme du début.

Pouvez-vous m'expliquer les questions 3 et 4 svp? notamment pour particulier Sn