Vecteur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nj-MI
- Messages: 5
- Enregistré le: 05 Déc 2013, 16:36
-
 par Nj-MI » 05 Déc 2013, 16:45
par Nj-MI » 05 Déc 2013, 16:45
Bonjour a tous,
Je suis en première licence en maathématique informatique et je ne comprend pas certaine chose.

Dans mon cours intitulé géometrie et polynome je ne comprend pas comment résoudre cette exercice:
soit u et v deux vecteur non colinéaire du plan
a) demontré qu'il existe un nombre reel
a et un seul tel que le vecteur h(vecteur) = au(u vecteur) + (1-a) soit orthogonal à V-U ( tout deux vecteurs)
b) demontrer que si u et v sont orthogonaux alors
||h|| ||v-u|| = ||u|| ||v|| ( toute les lettre sont indiquer comme des vecteur)
Merci d'avance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2013, 21:23
par Ben314 » 05 Déc 2013, 21:23
Salut,
a) Pour que deux vecteurs soient orthogonaux il faut (et il suffit) que le produit scalaire des deux fasse 0.
Ici, ça va te faire une équation du premier degrés en a...
b) Une fois que tu aura la valeur de a (donc l'expression du vecteur h), c'est une simple vérification.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nj-MI
- Messages: 5
- Enregistré le: 05 Déc 2013, 16:36
-
 par Nj-MI » 06 Déc 2013, 10:36
par Nj-MI » 06 Déc 2013, 10:36
une mise en equation? mon scalaire serait alors a? et comment pourrais trouver a alors que je n'ai aucune donnée?
Merci. :we:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Déc 2013, 11:25
par chan79 » 06 Déc 2013, 11:25
Nj-MI a écrit:une mise en equation? mon scalaire serait alors a? et comment pourrais trouver a alors que je n'ai aucune donnée?
Merci. :we:
salut
tu as comme données les vecteurs

et

Comme te l'a proposé Ben314, écris que le produit scalaire est nul
tu dois avoir

-
Nj-MI
- Messages: 5
- Enregistré le: 05 Déc 2013, 16:36
-
 par Nj-MI » 06 Déc 2013, 11:54
par Nj-MI » 06 Déc 2013, 11:54
Pourrais tu mettre le détaille de l'équation stp? et ou est passer le H?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Déc 2013, 14:24
par chan79 » 06 Déc 2013, 14:24
Nj-MI a écrit:Pourrais tu mettre le détaille de l'équation stp? et ou est passer le H?
=0)
-
Nj-MI
- Messages: 5
- Enregistré le: 05 Déc 2013, 16:36
-
 par Nj-MI » 07 Déc 2013, 14:26
par Nj-MI » 07 Déc 2013, 14:26
mise en equation:
a \vec{u}+ (1-a) \vec{v} = (\vec{v} - \vect{u})
par contre je ne vois pas comment tu arriver avec les carée
ou bien l'eaquation serais ca : a \vec{u}+ (1-a) \vec{v} = (\vec{v} - \vect{u}) \vec{h}
et on developpe \vec{h} = a \vec{u}+ (1-a) \vec{v}
Mais malgré ca je n'arrive pas a avoir la solution de a.
Merci
-
Nj-MI
- Messages: 5
- Enregistré le: 05 Déc 2013, 16:36
-
 par Nj-MI » 07 Déc 2013, 14:30
par Nj-MI » 07 Déc 2013, 14:30
mise en equation:
[TEX] a \vec{u}+ (1-a) \vec{v} = (\vec{v} - \vect{u}) [\TEX]
par contre je ne vois pas comment tu arriver avec les carée
ou bien l'eaquation serais ca : [TEX]a \vec{u}+ (1-a) \vec{v} = (\vec{v} - \vect{u}) \vec{h} [\TEX]
et on developpe [TEX] \vec{h} = a \vec{u}+ (1-a) \vec{v}[\TEX]
Mais malgré ca je n'arrive pas a avoir la solution de a.
Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 14:37
par Ben314 » 07 Déc 2013, 14:37
Tu ne veut pas que les vecteurs soient
égaux mais qu'ils soient
orthogonaux.
Donc l'équation, ce n'est pas ça :
Nj-MI a écrit: \vec{v} = (\vec{v} - \vec{u}))
mais ça :
 \vec{v}\big).(\vec{v} - \vec{u})=0)
où le . désigne le produit scalaire (qui peut aussi être noté )
Evidement, si tu préfère, tu peut écrire
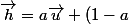 \vec{v}\)
et
=0)
, mais ça va pas changer grand chose... :doh:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Déc 2013, 14:43
par chan79 » 07 Déc 2013, 14:43
Tu pourrais d'abord prendre un exemple avec par exemple
)
et
)
.
a(1;2)+(1-a)(5;1)=(5-4a;1+a)
\vec{v}- \vec{u}=(4;-1)
on a l'orthogonalité si
4(5-4a)-(1+a)=0
20-16a-1-a=0
a=19/17
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
