Bonjour, j'ai un problème avec un exercice. On étudie f(x)=Arcsin((4x^3)-3x). Avec les questions préliminaires je dit que f est défini pour x compris entre -1 et 1. J'ai réussi à calculer la dérivée : (12x²-3)/(Racine(1-(4x^3-3x)²)) soit (g'(x)/(Racine(1-g(x)²)) qui est défnini pour x compris entre -1 et 1 avec x différent de -1,1,1/2 et -1/2. Ils demandent par la suite :
de montrer que si |x|<=(1/2) alors f(x)=-3Arcsin(x).
Pourriez-vous m'aider ? Merci d'avance.
Manier Arcsin(x)
6 messages
- Page 1 sur 1
frodelma a écrit:Bonjour, j'ai un problème avec un exercice. On étudie f(x)=Arcsin((4x^3)-3x). Avec les questions préliminaires je dit que f est défini pour x compris entre -1 et 1. J'ai réussi à calculer la dérivée : (12x²-3)/(Racine(1-(4x^3-3x)²)) soit (g'(x)/(Racine(1-g(x)²)) qui est défnini pour x compris entre -1 et 1 avec x différent de -1,1,1/2 et -1/2. Ils demandent par la suite :
de montrer que si |x|<=(1/2) alors f(x)=-3Arcsin(x).
Pourriez-vous m'aider ? Merci d'avance.
Une alternative à la proposition de Ben314:
Pour x vérifiant |x| <=1/2, |Arcsin(x)| <= pi/6 donc 3|Arcsin(x)| <= pi/2.
On clacule sin(3y) en fonction de sin(y): sin(3y) = 3siny - 4sin^3(y).
Si on pose x = siny on a 3y = Arcsin(3x - 4x^3), ce qui donne:
3Arcsin(x) = Arcsin(3x - 4x^3) donc f(x) = -3Arcsin(x)
Il y a des tonnes de "racines évidentes" :
^2=(1-3x+4x^3)(1+3x-4x^3))
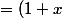(1-4x+4x^2)(1-x)(1+4x+4x^2))
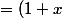(1-2x)^2(1-x)(1+2x)^2)
Et, aprés simplification, tu tombe sur=\frac{\pm3}{\sqrt{1-x^2}) , le signe étant celui de
, le signe étant celui de 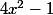
Je t'inciterais vivement à utiliser cette méthode (à priori celle attendue dans l'exercice) ET AUSSI celle mrif qui permet elle de comprendre pourquoi ton f' se simplifie aussi "miraculeusement".
Voire même, si tu as un peu de temps, à regarder ce que vaut la fonction f sur [1/2,1] et/ou sur [-1,-1/2] en utilisant les deux méthodes.
Et, aprés simplification, tu tombe sur
Je t'inciterais vivement à utiliser cette méthode (à priori celle attendue dans l'exercice) ET AUSSI celle mrif qui permet elle de comprendre pourquoi ton f' se simplifie aussi "miraculeusement".
Voire même, si tu as un peu de temps, à regarder ce que vaut la fonction f sur [1/2,1] et/ou sur [-1,-1/2] en utilisant les deux méthodes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
