Bonjour, je n'ai pas compris comment on calcule les racine d'un nombre complexe comme z au cube=2+2i ou z au cube=8i.
Pourriez vous m'expliquer s'il vous plait?
Question sur les racine
6 messages
- Page 1 sur 1
Si z=a+bi, on écrit le nombre sous la forme exponentielle:
})
où
et) + un ajustement pour l'angle dans le bon quadrant:
+ un ajustement pour l'angle dans le bon quadrant:
si a>0 et b>0 pas d'ajustement
a>0 et b0 ou a<0 et b<0): + pi
Ensuite on élève à la puissance 1/n:
}{n}})
et pour avoir toutes les racines, on calcule successivement l'exposant de exp() pour les valeurs de k=0,1,2...n-1.
Ensuite, si on veut remettre sous la forme cartésienne chaque racine, on utilise la formule bien connue:
 + i sin(\theta) ))
(Évidemment, on prend n=3 pour la racines cubiques, n=2 pour les racines carrées, etc.)
où
et
si a>0 et b>0 pas d'ajustement
a>0 et b0 ou a<0 et b<0): + pi
Ensuite on élève à la puissance 1/n:
et pour avoir toutes les racines, on calcule successivement l'exposant de exp() pour les valeurs de k=0,1,2...n-1.
Ensuite, si on veut remettre sous la forme cartésienne chaque racine, on utilise la formule bien connue:
(Évidemment, on prend n=3 pour la racines cubiques, n=2 pour les racines carrées, etc.)
Juste une remarque dans un cas particulier où l'on peut trouver une racine "évidente" z1, les autres racines sont z1*j et z1*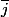 où j est la racine cubique de l'unité bien connue, c'est à dire :
où j est la racine cubique de l'unité bien connue, c'est à dire : 
Par exemple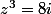 a pour racine évidente -2i , donc les autres racines sont -2i*j et -2i*
a pour racine évidente -2i , donc les autres racines sont -2i*j et -2i*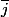 .
.
 a pour racine évidente (1+i) , donc les autres racines sont (1+i)*j et (1+i)*
a pour racine évidente (1+i) , donc les autres racines sont (1+i)*j et (1+i)*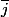 .
.
Par exemple
Ok merci ,et si j'ai bien compris,les racine cubique de z1=2+2i sont:
zk= racine cubique de|z|exp( ;)/n+2k;)/n) donc pour k= 0,
zo = (racine cubique de 2;)2)exp(;) /12+2*0;)/3)= (racine cubique de 2;)2)exp(;) /12)
pour k=1,z1= (racine cubique de 2;)2)exp(;) /12+2*1;)/3)=(racine cubique de 2;)2)exp(3;) /4)
Enfin pour k=2,z2=(racine cubique de 2;)2)exp(;) /12+2*2*;)/3)= (racine cubique de 2;)2)exp(17;) /12).
zk= racine cubique de|z|exp( ;)/n+2k;)/n) donc pour k= 0,
zo = (racine cubique de 2;)2)exp(;) /12+2*0;)/3)= (racine cubique de 2;)2)exp(;) /12)
pour k=1,z1= (racine cubique de 2;)2)exp(;) /12+2*1;)/3)=(racine cubique de 2;)2)exp(3;) /4)
Enfin pour k=2,z2=(racine cubique de 2;)2)exp(;) /12+2*2*;)/3)= (racine cubique de 2;)2)exp(17;) /12).
penny a écrit: pour k=1,z1= (racine cubique de 2;)2)exp(;) /12+2*1;)/3)=(racine cubique de 2;)2)exp(3;) /4)
En fait z1 = -1 + i
donc les deux autres sont z1*j et z1*
Multiplier par j revient à ajouter (2pi)/3 à l'argument sans modifier le module et multiplier par
Ceci est important si l'on souhaite présenter ces racines sous forme algébrique.
D'autre part dans vos réponses comme
Dans le cas particulier de la racine carrée, il existe une méthode qui évite de passer par les formes exponentielles.
On cherche une racine carrée de a+ib.
C'est-à-dire : On cherche x et y réels tels que (x+iy)²=a+ib.
On développe l'équation et on identifie les parties réelles et imaginaires.
On obtient :
(1) : x²-y²=a
(2) : 2xy=b
On utilise ensuite l'égalité des modules :
(3) x²+y²=;)(a²+b²)
Le système composé par les équations (1) et (3) est facile à résoudre. On trouve alors x² et y². On résout le problème de signe avec l'équation (2) qui donne le signe de y en fonction de celui de x.
On cherche une racine carrée de a+ib.
C'est-à-dire : On cherche x et y réels tels que (x+iy)²=a+ib.
On développe l'équation et on identifie les parties réelles et imaginaires.
On obtient :
(1) : x²-y²=a
(2) : 2xy=b
On utilise ensuite l'égalité des modules :
(3) x²+y²=;)(a²+b²)
Le système composé par les équations (1) et (3) est facile à résoudre. On trouve alors x² et y². On résout le problème de signe avec l'équation (2) qui donne le signe de y en fonction de celui de x.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
