Limite math

[loujouni]

Bonjour alors voilà mon prof de math m'a donné cette limite et il ma dit que la reponse sera 0 alors que jai -3/2 comme resultat !!
la limite est :


lim ( quand x tend vers + l'infini) de : racine(x^3)/x+3) - x

( (racine de x au cube sur (x+3)) moins x)




merci de me repondre vite

[MMu]

Utilise ... :zen:

[loujouni]

Cest ce que j'ai fait mais si vous pouviez la calculer svp, ca serait gentil.

[titine]

Bonjour alors voilà mon prof de math m'a donné cette limite et il ma dit que la reponse sera 0 alors que jai -3/2 comme resultat !!
la limite est :


lim ( quand x tend vers + l'infini) de : racine(x^3)/x+3) - x

( (racine de x au cube sur (x+3)) moins x

C'est bien rac(x^3) / (x+3) - x ?
Ou rac(x^3/(x+3)) - x ?

[loujouni]

cest la dexieme option :
cest la racine(x^3/x+3) seulement le tout - x
merci de me donner le resultat

[porkynou]

Bonsoir,
Rentre ta fonction dans la calculatrice, tu verras que :
lim qd x tend vers 0 = 0
lim qd x tend ves + l'infini = -3/2
Je n'arrive pas à retrouver ce résultat, peux-tu expliquer ton calcul stp?

[loujouni]

Bonsoir, je ne pense que ma calculatrice soit programmée pour calculer les limites
alors jai utilisé la relation a-b=a²-b²/a+b

[Carpate]

Bonsoir, je ne pense que ma calculatrice soit programmée pour calculer les limites
alors jai utilisé la relation a-b=a²-b²/a+b

De toute façon ce n'est pas ta calculette qui doit trouver le résultat mais toi :
: mult. par quantité conjuguée
qui tend vers quand

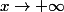
[loujouni]

Merci beaucoup Carpate