Exercice non compris
12 messages
- Page 1 sur 1
Exercice non compris
Bonjour/Bonsoir !
Je suis en 1S et j'ai un devoir maison à rendre, j'ai fais tous les exercices sauf un où je bloque totalement car je ne comprends pas.. Sa peut paraitre bête comme exercice pour certains mais tant pis ! Merci à ceux qui prendrons un peu de leur temps pour me faire comprendre/m'aider :)
Voici mon énoncé:
Le plan est rapporté à un repère orthonormé (o, vecteur i, vecteur j), l'unité de longueur est le cm. On considère le point A et B de coordonnées respectives (-3;2) et (1;1) et le point I milieu du segment [AB].
1) En utilisant le fait qu'un point M(x;y) appartient au cercle (C) de diamètre [AB] si et seulement si IM=IA, démontrer qu'une équation de ce cercle est: x²+y²+2x-3y-1=0
2a) p désigne un nombre réel. On considère la droite (Dp) d'équation y=-2x+p.
2b) Etudier l'intersection du cercle et de sa droite (D3).
3a)Démontrer que les abscisses des points communs à (C) et à (Dp) sont les solutions de l'équation: 5x²+(8-4p)x+p²-3p-1=0.
3b) Déterminer, suivant les valeurs de p, le nombre de points communs à (C) et à (Dp).
4) Déterminer une équation de chacune des tangentes à (C) de coefficient directeur -2.
Voilà, je sais que c'est beaucoup, mais je demande juste à ce qu'on m'explique car je suis vraiment perdue pour cet exercice :mur:
Merci encore !
Je suis en 1S et j'ai un devoir maison à rendre, j'ai fais tous les exercices sauf un où je bloque totalement car je ne comprends pas.. Sa peut paraitre bête comme exercice pour certains mais tant pis ! Merci à ceux qui prendrons un peu de leur temps pour me faire comprendre/m'aider :)
Voici mon énoncé:
Le plan est rapporté à un repère orthonormé (o, vecteur i, vecteur j), l'unité de longueur est le cm. On considère le point A et B de coordonnées respectives (-3;2) et (1;1) et le point I milieu du segment [AB].
1) En utilisant le fait qu'un point M(x;y) appartient au cercle (C) de diamètre [AB] si et seulement si IM=IA, démontrer qu'une équation de ce cercle est: x²+y²+2x-3y-1=0
2a) p désigne un nombre réel. On considère la droite (Dp) d'équation y=-2x+p.
2b) Etudier l'intersection du cercle et de sa droite (D3).
3a)Démontrer que les abscisses des points communs à (C) et à (Dp) sont les solutions de l'équation: 5x²+(8-4p)x+p²-3p-1=0.
3b) Déterminer, suivant les valeurs de p, le nombre de points communs à (C) et à (Dp).
4) Déterminer une équation de chacune des tangentes à (C) de coefficient directeur -2.
Voilà, je sais que c'est beaucoup, mais je demande juste à ce qu'on m'explique car je suis vraiment perdue pour cet exercice :mur:
Merci encore !
Salut !
Qu'as-tu fait pour le moment ?
PetiteFraise a écrit:Bonjour/Bonsoir !
Je suis en 1S et j'ai un devoir maison à rendre, j'ai fais tous les exercices sauf un où je bloque totalement car je ne comprends pas.. Sa peut paraitre bête comme exercice pour certains mais tant pis ! Merci à ceux qui prendrons un peu de leur temps pour me faire comprendre/m'aider
Voici mon énoncé:
Le plan est rapporté à un repère orthonormé (o, vecteur i, vecteur j), l'unité de longueur est le cm. On considère le point A et B de coordonnées respectives (-3;2) et (1;1) et le point I milieu du segment [AB].
1) En utilisant le fait qu'un point M(x;y) appartient au cercle (C) de diamètre [AB] si et seulement si IM=IA, démontrer qu'une équation de ce cercle est: x²+y²+2x²-3y-1=0
2a) p désigne un nombre réel. On considère la droite (Dp) d'équation y=-2x+p.
2b) Etudier l'intersection du cercle et de sa droite (D3).
3a)Démontrer que les abscisses des points communs à (C) et à (Dp) sont les solutions de l'équation: 5x²+(8-4p)x+p²-3p-1.
3b) Déterminer, suivant les valeurs de p, le nombre de points communs à (C) et à (Dp).
4) Déterminer une équation de chacune des tangentes à (C) de coefficient directeur -2.
Voilà, je sais que c'est beaucoup, mais je demande juste à ce qu'on m'explique car je suis vraiment perdue pour cet exercice :mur:
Merci encore !
Qu'as-tu fait pour le moment ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Salut !
Ton énoncé est tourné bizarrement : la question 2°)a) n'en est pas une :hein:
Je pense plutôt que l'équation de) est
est  , non ?
, non ?
Soit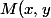) un point commun à
un point commun à ) et
et ) .
.
Alors dans ce cas, \in (\mathcal{C}) \\ M(x,y)\in (D_p) } \Longleftrightarrow { \{ x^2+y^2+2x-3y-1=0 \\ y= -2x+p }) .
.
Remplace dans la première ligne y par sa valeur donnée en deuxième ligne :+++:
PetiteFraise a écrit:Bonjour/Bonsoir !
Je suis en 1S et j'ai un devoir maison à rendre, j'ai fais tous les exercices sauf un où je bloque totalement car je ne comprends pas.. Sa peut paraitre bête comme exercice pour certains mais tant pis ! Merci à ceux qui prendrons un peu de leur temps pour me faire comprendre/m'aider
Voici mon énoncé:
Le plan est rapporté à un repère orthonormé (o, vecteur i, vecteur j), l'unité de longueur est le cm. On considère le point A et B de coordonnées respectives (-3;2) et (1;1) et le point I milieu du segment [AB].
1) En utilisant le fait qu'un point M(x;y) appartient au cercle (C) de diamètre [AB] si et seulement si IM=IA, démontrer qu'une équation de ce cercle est: x²+y²+2x²-3y-1=0
2a) p désigne un nombre réel. On considère la droite (Dp) d'équation y=-2x+p.
2b) Etudier l'intersection du cercle et de sa droite (D3).
3a)Démontrer que les abscisses des points communs à (C) et à (Dp) sont les solutions de l'équation: 5x²+(8-4p)x+p²-3p-1.
3b) Déterminer, suivant les valeurs de p, le nombre de points communs à (C) et à (Dp).
4) Déterminer une équation de chacune des tangentes à (C) de coefficient directeur -2.
Voilà, je sais que c'est beaucoup, mais je demande juste à ce qu'on m'explique car je suis vraiment perdue pour cet exercice :mur:
Merci encore !
Ton énoncé est tourné bizarrement : la question 2°)a) n'en est pas une :hein:
Je pense plutôt que l'équation de
Soit
Alors dans ce cas,
Remplace dans la première ligne y par sa valeur donnée en deuxième ligne :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Ton énoncé est tourné bizarrement : la question 2°)a) n'en est pas une :hein:
Je pense plutôt que l'équation deest
, non ?
Soitun point commun à
et
.
Alors dans ce cas,.
Remplace dans la première ligne y par sa valeur donnée en deuxième ligne :+++:
Regarde la question 3°)a).
Est-ce que ça ressemble à ce qu'on te demande ? :lol3:
J'ai peut-être été peu précis : à partir de l'égalité
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Regarde la question 3°)a).
Est-ce que ça ressemble à ce qu'on te demande ? :lol3:
J'ai peut-être été peu précis : à partir de l'égalité, remplace
par son expression donnée dans la deuxième ligne, c'est-à-dire remplace y par
A chaque fois, je tombe sur un résultat différent, je ne comprends pas, je dois sûrement faire une faute de calcul !
PetiteFraise a écrit:Je tombe presque sur le même calcule , à part que je n'ai pas (8-4p)x mais -2xp
Cale vient du fait que tu as mal développé, mais pas de soucis :lol3:
Prenons
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
PetiteFraise a écrit:Ma faute est ici : 2y= 4x^2+p^2
(Je présume que tu veux parler de y^2 ? )
Oui ! Ca pique les yeux :ptdr:
Suivant ta logique :
On dirait que tu ne connais pas l'identité remarquable
Mais ça n'est pas grave. Ce qui est dommage, c'est que tu pourrais la retrouver par le calcul :we:
Calcule
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:(Je présume que tu veux parler de y^2 ? )
Oui ! Ca pique les yeux :ptdr:
Suivant ta logique :donc
:ptdr:
On dirait que tu ne connais pas l'identité remarquable... car malheureusement, le carré ne se distribue pas par rapport à l'addition ici (
).
Mais ça n'est pas grave. Ce qui est dommage, c'est que tu pourrais la retrouver par le calcul :we:
Calcule, puis fais de même avec
:+++:
J'avais fais comme ça au départ mais comme je n'arrivais toujours pas au bon résultat je me suis dis que c'etait faux
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
