Dm de Maths Terminale !

[pb.mgf]

Bonjour, je viens demander de l'aide car je n'arrive pas à finir mon dm de maths... Merci à tous ceux qui m'aideront !

ex:
Dans le cas suivants, on considère une fonction f et sa représentation graphique C dans un repère orthonormal.

1) Déterminer les limites de la fonction f aux bornes de son ensemble de définition
En déduire les (éventuelles) asymptotes à la courbe C parallèles aux axes de coordonnées.

f est la fonction définie sur R-{1, 1} par f(x) = (x^5 2x^3+2x2+2x 3) / (x^4 - 1)

[busard_des_roseaux]

bonjour,

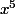
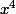
factorise par au numérateur et au dénominateur

simplifie dans la somme les termes comme

[landagama]

Comme f est définie sur R\{-1;1}, les bornes de son ensemble de définition sont donc : - ; -1 ; 1 et tu es d'accord ?
Il faut chercher les limites de f lorsque x tend vers ces 4 bornes.
En l'infini, tu dois factoriser f par x^5 en haut et par x^4 en bas (les plus hauts degrés), commence déjà par ça.

[pb.mgf]

Oui, je suis d'accord, donc si je factorise comme vous me l'avez dit, j'ai trouvé çà :

X facteur de ((1 - 2/X^2 + 2/X^3 + 2/X^4 - 3/X^5)/(1 - 1/X^4)

[busard_des_roseaux]

ok, on peut faire le calcul de limite quand X tend vers

[landagama]

Ta factorisation est bonne, tu dois maintenant calculer la limite en -l'infini puis en +l'infini des 3 termes qui interviennent, à savoir :
- limite de x
- limite de
- et limite de
puis de regrouper les résultats pour avoir la limite de f(x), ça va ?

[pb.mgf]

La limite de f quand X tend vers +l'infini = +l'infini

car quand X tend vers +l'infini :
lim X = +l'infini
lim de (1 - 2/X^2 + 2/X^3 + 2/X^4 - 3/X^5) = 1
et lim (1 - 1/X^4) = 1

et la limite de f quand X tend vers -l'infini = -l'infini

car quand X tend vers -l'infini :
car lim X = -l'infini
lim de (1 - 2/X^2 + 2/X^3 + 2/X^4 - 3/X^5) = 1
et lim (1 - 1/X^4) = 1

[landagama]

c'est bien ça !

[pb.mgf]

Donc pour continuer l'exercice je dois trouver les limites quand X tend vers 1 et -1 ?

[landagama]

oui c'est ça

[pb.mgf]

Merci beaucoup pour votre aide, j'ai fini l'exercice et je l'ai compris ! :)

[landagama]

Ben alors super ! Je t'invite à aller consulter mon site (qui en est encore à ses débuts !) si tu as des petits problèmes mathématiques !
Bonne continuation à toi.

[tototo]

Bonjour, je viens demander de l'aide car je n'arrive pas à finir mon dm de maths... Merci à tous ceux qui m'aideront !

ex:
Dans le cas suivants, on considère une fonction f et sa représentation graphique C dans un repère orthonormal.

1) Déterminer les limites de la fonction f aux bornes de son ensemble de définition
En déduire les (éventuelles) asymptotes à la courbe C parallèles aux axes de coordonnées.

f est la fonction définie sur R-{1, 1} par f(x) = (x^5 2x^3+2x2+2x 3) / (x^4 - 1)

Bonjour

Lim(x- +infini) f ( x)=+infini
lim ( x->-infini) f (x)=-infini car f prend la limite de son terme de plus haut degre : x^5/x^4=x