Bonjour. Je n'arrive pas à résoudre un exercice sur les complexes. Pourriez-vous m'aider svp ?
Voici l'énoncé:
Soit l'équation E-> z³+(2-2i)z²+(5-4i)z-10i=0
-> Démontrer que E possède une solution imaginaire pure.
-> Déterminer les complexes A et B tels que pour tout complexe z, E=(z-2i)(z²+Az+B)
-> Résoudre E dans C
Je vous remercie d'avance !
Exercice difficile sur les complexes.
4 messages
- Page 1 sur 1
Salut !
1°/ On te dit que E admet une solution imaginaire pure : soit cette solution.
cette solution.
Dans ce cas, vérifie
vérifie  i.e.
i.e. ^3+(2-2i)(bi)^2+(5-4i)bi-10i=0) .
.
Essaye alors de trouver :++:
:++:
(La deuxième question te donne la réponse attendue : tu dois trouver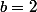 .
.
On a donc déjà une solution :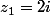 .)
.)
2°/ Développe(z^2+Az+B)) puis identifie terme à terme les coefficients avec
puis identifie terme à terme les coefficients avec z^3+(5-4i)z-10i) .
.
3°/ Cela revient à résoudre (pour et
et  trouvé),
trouvé),  .
.
amimilad654321 a écrit:Bonjour. Je n'arrive pas à résoudre un exercice sur les complexes. Pourriez-vous m'aider svp ?
Voici l'énoncé:
Soit l'équation E-> z³+(2-2i)z²+(5-4i)z-10i=0
-> Démontrer que E possède une solution imaginaire pure.
-> Déterminer les complexes A et B tels que pour tout complexe z, E=(z-2i)(z²+Az+B)
-> Résoudre E dans C
Je vous remercie d'avance !
1°/ On te dit que E admet une solution imaginaire pure : soit
Dans ce cas,
Essaye alors de trouver
(La deuxième question te donne la réponse attendue : tu dois trouver
On a donc déjà une solution :
2°/ Développe
3°/ Cela revient à résoudre (pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
1°/ On te dit que E admet une solution imaginaire pure : soitcette solution.
Dans ce cas,vérifie
i.e.
.
Essaye alors de trouver:++:
(La deuxième question te donne la réponse attendue : tu dois trouver.
On a donc déjà une solution :.)
2°/ Développepuis identifie terme à terme les coefficients avec
.
3°/ Cela revient à résoudre (pouret
trouvé),
.
Expliqué comme ça, ça parait simple... Je vais réessayer, merci !
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
