Probleme suites numeriques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
charlotte44
- Membre Naturel
- Messages: 14
- Enregistré le: 15 Mai 2013, 18:42
-
 par charlotte44 » 02 Oct 2013, 15:23
par charlotte44 » 02 Oct 2013, 15:23
Bonjour,
j'ai un problème avec cet exercice ;
Soit f la fonction de R \ {;);)2,;)2} dans R dé;)nie par f(x) = x²/(2-x²)
. Soit u0 ;) [0,1[. On dé;)nit par récurrence la suite (un)n;)N qui véri;)e, pour tout
n ;) N, un+1 = f(un).
1. Montrer que pour tout x ;) [0,1[, f(x) ;) [0,1[ et en déduire que la suite (un)n;)N est
bien dé;)nie.
2-Montrer que (un)n;)N décroît.
3. En déduire que la suite (un)n;)N converge.
4. Quelle est sa limite ?
5. On suppose maintenant u0 = 1. Que peut-on dire de la suite (un)n;)N ?
pour le 1 j'ai fait :
-soit x appartient à [0,1], puisque 0recurrence pour montrer que la suite est definie :
- puisque U0 appartient a [0,1] donc U0>0 donc vrai
- on suppose la propriété vraie au rang n, montrons qu'elle reste vraie au rang n+1
n²/(2-n²)>0 d'ou Un+1>0 donc la suite est bien définie
mais pour la question 2 , je ne comprends pas ce qu'est Un, je pensais que c'etait n²/(2-n²), mais elle est croissante..et non dé"croissante
Merci pour votre aide.
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 02 Oct 2013, 15:33
par siger » 02 Oct 2013, 15:33
bonjour
un = (u(n-1)^2/(2-u(n-1)^2) et non un n^2/(2-n^2))
-
charlotte44
- Membre Naturel
- Messages: 14
- Enregistré le: 15 Mai 2013, 18:42
-
 par charlotte44 » 02 Oct 2013, 15:45
par charlotte44 » 02 Oct 2013, 15:45
d'accord, et donc pour prouver quelle décroit comment puis je faire?
j'ai essayé Un+1-Un mais ça ne donne rien d'interessant..
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 02 Oct 2013, 16:03
par siger » 02 Oct 2013, 16:03
re
tu utilises la question 1 et les proprietes de f(x)
....
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 02 Oct 2013, 17:19
par Maxmau » 02 Oct 2013, 17:19
charlotte44 a écrit:d'accord, et donc pour prouver quelle décroit comment puis je faire?
j'ai essayé Un+1-Un mais ça ne donne rien d'interessant..
Bj
Mais si!!
Un+1 - Un = f(Un) - f(Un-1) = (Un - Un-1)f'(c) où c entre Un-1 et Un (th des AF)
autre méthode: étudie le signe de f(x) - x d'où le signe de f(Un) - Un
-
charlotte44
- Membre Naturel
- Messages: 14
- Enregistré le: 15 Mai 2013, 18:42
-
 par charlotte44 » 02 Oct 2013, 19:31
par charlotte44 » 02 Oct 2013, 19:31
Bonsoir;
j'ai compris le principe pour montrer qu'une suite est decroissante ou croissante,
j'ai essayé de faire f(Un)-Un ce qui donne n²/(2-n²) - U(n-1)²/(2-U(n-1))
mais je ne vois pas comment je pourrais le simplifier pour ainsi conclure..
il faut que je développe les identités remarquables?
-
charlotte44
- Membre Naturel
- Messages: 14
- Enregistré le: 15 Mai 2013, 18:42
-
 par charlotte44 » 02 Oct 2013, 19:47
par charlotte44 » 02 Oct 2013, 19:47
j'ai fais f(Un)-Un , ça donne Un²/(2-Un²) - Un = ( Un²-2Un-Un^3)/(2-Un²)
= - (Un^3 - Un²+ 2Un)/2-Un² ce qui est <0 elle est donc décroissante?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 02 Oct 2013, 21:56
par Maxmau » 02 Oct 2013, 21:56
charlotte44 a écrit:j'ai fais f(Un)-Un , ça donne Un²/(2-Un²) - Un = ( Un²-2Un-Un^3)/(2-Un²)
= - (Un^3 - Un²+ 2Un)/2-Un² ce qui est <0 elle est donc décroissante?
OK mais il faut justifier que la quantité est negative
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 03 Oct 2013, 00:07
par deltab » 03 Oct 2013, 00:07
Bonsoir.
@charlotte44
Pourquoi n'as tu pas suivi le conseil de Maxmau concernant l'autre méthode (étudier la fonction
=f(x)-x)
) , l'étude du signe de
)
est plus aisé que le signe de
=f(U_n)-U_n=U_{n+1}-U_n)
.
-
charlotte44
- Membre Naturel
- Messages: 14
- Enregistré le: 15 Mai 2013, 18:42
-
 par charlotte44 » 03 Oct 2013, 17:51
par charlotte44 » 03 Oct 2013, 17:51
deltab a écrit:Bonsoir.
@charlotte44
Pourquoi n'as tu pas suivi le conseil de Maxmau concernant l'autre méthode (étudier la fonction
=f(x)-x)
) , l'étude du signe de
)
est plus aisé que le signe de
=f(U_n)-U_n=U_{n+1}-U_n)
.
Bonjour,
si je fais f(x)-x ça me donne x²/(2-x) - x je sais que f(x) est croissante ( j'ai fais la dérivée.. ) donc f(x)> x et donc Un decroit? est ce bien ça?..
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Oct 2013, 17:22
par deltab » 04 Oct 2013, 17:22
Bonjour
charlotte44 a écrit:Bonjour,
si je fais f(x)-x ça me donne x²/(2-x) - x je sais que f(x) est croissante ( j'ai fais la dérivée.. ) donc f(x)> x et donc Un decroit? est ce bien ça?..
C'est le signe de f(x)-x qui nous intéresse le plus pas celui de f.
Le fait que f est strictement croissante nous donne ici vu que f(0)=0, f(x)>=0 c'est à dire le signe de f(x) pas celui de f(x)-x.
Si
-x>0)
, la suite récurrente
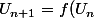)
serait d'après toi décroissante,
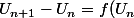-U_n)
est >0 ou <0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
