(non résolu) Equations Différentielles L3 Mécanique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 26 Sep 2013, 18:05
par Ge3r1 » 26 Sep 2013, 18:05
Bonjour,
Actuellement en L3 je rencontre des problèmes quant à la résolution de cet exercice :
[CENTER]
Exercice [/CENTER]
Réponse trouvée à la question 1 :
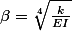
Pour la question 2, je dois trouver les valeurs A et B,
J'ai trouver dv/dx :
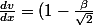exp(\frac{-\beta x}{\sqrt{2}})[(A+\frac{\beta B}{\sqrt{2}})cos(\frac{\beta x}{\sqrt{2}})+(B-\frac{\beta A}{\sqrt{2}})sin(\frac{\beta x}{\sqrt{2}})])
On applique ensuite le fait

:
A=B \beta(\frac{-\sqrt{2}+\beta }{2}))
Mais je ne sais pas comment m'en sortir pour la suite, si quelqu'un pouvait me donner un coup de pouce ce serait parfait !!
Merci d'avance

-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 26 Sep 2013, 19:01
par Sourire_banane » 26 Sep 2013, 19:01
Salut,
Ge3r1 a écrit:Bonjour,
Actuellement en L3 je rencontre des problèmes quant à la résolution de cet exercice :
[CENTER]
Exercice [/CENTER]
Réponse trouvée à la question 1 :
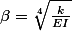
Pour la question 2, je dois trouver les valeurs A et B,
J'ai trouver dv/dx :
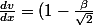exp(\frac{-\beta x}{\sqrt{2}})[(A+\frac{\beta B}{\sqrt{2}})cos(\frac{\beta x}{\sqrt{2}})+(B-\frac{\beta A}{\sqrt{2}})sin(\frac{\beta x}{\sqrt{2}})])
On applique ensuite le fait

:
A=B \beta(\frac{-\sqrt{2}+\beta }{2}))
Mais je ne sais pas comment m'en sortir pour la suite, si quelqu'un pouvait me donner un coup de pouce ce serait parfait !!
Merci d'avance

J'ai rien vérifié.
Ben maintenant tu dérives trois fois v et tu formes un système pour trouver A et B.
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 26 Sep 2013, 19:19
par Ge3r1 » 26 Sep 2013, 19:19
J'ai essayé mais cela donne des équations à rallonge un peu, il ne faut pas plutôt se resservir des équations données au début de l'énoncé ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 26 Sep 2013, 19:23
par Sourire_banane » 26 Sep 2013, 19:23
J'en sais rien, mais normalement t'as besoin que des conditions initiales, car la solution est typique d'un ordre 2...
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 26 Sep 2013, 19:35
par Ge3r1 » 26 Sep 2013, 19:35
Ok bah je vais essayer merci !
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 27 Sep 2013, 07:33
par Ge3r1 » 27 Sep 2013, 07:33
Deriver trois fois ne donne pas une solution exploitable facilement. Quelqu'un aurait il une autre solution ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 27 Sep 2013, 08:01
par ampholyte » 27 Sep 2013, 08:01
Bonjour,
Comme l'a dit Sourire_banane, tu peux trouver la solution à partir des deux conditions aux limites que l'on te donne.
Peut-être as-tu fait des erreurs dans tes calculs. Serait-il possible d'avoir le détail de tes calculs ?
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 27 Sep 2013, 19:29
par Ge3r1 » 27 Sep 2013, 19:29
ampholyte a écrit:Bonjour,
Comme l'a dit Sourire_banane, tu peux trouver la solution à partir des deux conditions aux limites que l'on te donne.
Peut-être as-tu fait des erreurs dans tes calculs. Serait-il possible d'avoir le détail de tes calculs ?
Donc voilà je vais vous mettre ce que j'ai trouvé, s'il faut que je détaille en plus les calculs redites moi :
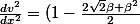exp(\frac{-\beta x}{\sqrt{2}})[(A+\frac{2\beta B}{\sqrt{2}}-\frac{A\beta^2}{2})cos(\frac{\beta x}{\sqrt{2}})+(B-\frac{2\beta A}{\sqrt{2}}-\frac{B\beta^2}{2})sin(\frac{\beta x}{\sqrt{2}})])
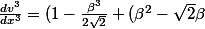)exp(\frac{-\beta x}{\sqrt{2}})[(A+\frac{3\beta B}{\sqrt{2}}-\frac{3A\beta^2}{2}-\frac{\beta^3 B}{2\sqrt{2}})cos(\frac{\beta x}{\sqrt{2}})+(B-\frac{3\beta A}{\sqrt{2}}-\frac{3B\beta^2}{2}+\frac{\beta^3 A}{2\sqrt{2}})sin(\frac{\beta x}{\sqrt{2}})]=\frac{-Q}{2EI})
On applique ensuite le fait

:
+B(\frac{12\beta-24\beta^2+10\sqrt{2}\beta^3-6\beta^4-2\sqrt{2}\beta^5+\beta^6}{8}))
-
Ge3r1
- Messages: 6
- Enregistré le: 26 Sep 2013, 17:22
-
 par Ge3r1 » 29 Sep 2013, 17:17
par Ge3r1 » 29 Sep 2013, 17:17
? pas d'avis
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
