Exercice suite Terminale S

[GomHK]

Bonjour, j'ai un exercice pour lundi et je ne comprends pas... Merci d'avance pour votre aide..


On considère la suite (Un) définie par U1=0 et Un+1= 1/(2-Un) pour tout n>ou égal à 1.
Après avoir conjecturé la valeur de Un en fonction de n, pour tout n>ou égal à 1, démontrer votre conjecture.


Je ne comprends pas comment je peux faire une conjecture à partir de ça ?...

[chan79]

Bonjour, j'ai un exercice pour lundi et je ne comprends pas... Merci d'avance pour votre aide..


On considère la suite (Un) définie par U1=0 et Un+1= 1/(2-Un) pour tout n>ou égal à 1.
Après avoir conjecturé la valeur de Un en fonction de n, pour tout n>ou égal à 1, démontrer votre conjecture.


Je ne comprends pas comment je peux faire une conjecture à partir de ça ?...

calcule les premiers termes (en fractions)

[GomHK]

je trouve u2=1/2 ; u3=2/3 et u4= 3/4
et ensuite ?

[chan79]

je trouve u2=1/2 ; u3=2/3 et u4= 3/4
et ensuite ?

calcule en encore 5 ou 6; tu verras bien de quoi il retourne

[GomHK]

On voit que le dénominateur est toujours le même nombre que la valeur de Un que l'on cherche ? ex : u8=7/8 : u9=8/9
Et le numérateur est toujours le nombre d'avant..

[chan79]

On voit que le dénominateur est toujours le même nombre que la valeur de Un que l'on cherche ? ex : u8=7/8 : u9=8/9
Et le numérateur est toujours le nombre d'avant..

donc on peut conjecturer que

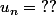
[GomHK]

On peut conjecturer que Un=n-1/n ?

[chan79]

On peut conjecturer que Un=n-1/n ?

oui, si c'est

Tu n'as plus qu'à le démontrer par récurrence

[GomHK]

oui, si c'est

Tu n'as plus qu'à le démontrer par récurrence

On pose P(n): Un= n-1/n

Par récurrence :

1) Initialisation

P(1) est-elle vraie ?
P(1): U1= (1-1)/1=0
U1=0, donc P(1) est vraie.

2) Hérédité

On suppose P(n) vraie pour tout n> ou égal à 1, et on veut démontrer que P(n+1) est vraie.
Je sais que Un= n-1/n, donc P(n+1)= (n+1)-1/n+1
On calcule Un+1=
Un+1= n+1-1/n+1= n-1/n

donc P(n+1) est vraie et d'après le théorème de récurrence, P(n) est vraie pour tout n> ou égal à 1.

C'est ça ?

[chan79]

il faut reprendre...
tu supposes et tu dois prouver

[GomHK]

je ne comprends pas..

[chan79]

je ne comprends pas..

tu sais que

Remplace par

[GomHK]

j'ai réussis, je trouve à la fin Un+1=n/n+1
Merci beaucoup !