Bloqué sur un problème...

[Axel0293]

Alors voilà je suis bloqué au bout de mon dm qui porte sur le second degré et je ne sais pas comment l'aborder je vous écrit l'énoncé :
Un champ rectangulaire a pour périmètre 80m quelles sont les dimensions de ce champ pour que son aire soit supérieure à 384m^2.
Si quelqu'un a des pistes il est le bienvenue :)

[John Difool]

Bonsoir,

quelles sont les formules du périmètre et de l'aire d'un rectangle de largeur et de longueur ?

[John Difool]

Bonsoir,

quelles sont les formules du périmètre et de l'aire d'un rectangle de largeur et de longueur ?

Essaie ensuite d'appliquer ces formules avec les données de ton problème.

[Axel0293]

Bonsoir,

quelles sont les formules du périmètre et de l'aire d'un rectangle de largeur et de longueur ?

Essaie ensuite d'appliquer ces formules avec les données de ton problème.

Pour le périmètre c'est lxl + LxL et pour l'Aire lxL mais y a t-il un rapport avec le second degré ?

[John Difool]

périmètre

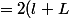Tu vas voir le rapport avec "le second degré" si tu essaies d'utiliser ces formules pour "modéliser" ton problème (;

[Axel0293]

C'est donc une inéquation supérieure ou égale à 384m^2 si je comprend bien ?

[John Difool]

Voilà,

Tu n'as plus qu'à étudier le signe de ton polynôme pour répondre au problème !

[Axel0293]

Malgré ça je bute toujours sur le contenu de l'inéquation, je dois sûrment pas être très doué...

[John Difool]

On a :

2(l+L) = 80 (1)
l*L > 384 (2)

(1) => L = 40-l

donc dans (2) : l*(40-l) > 384

Et tu peux mettre ça sous la forme d'un polynôme du second degré P(l) = a*l^2 +b*l + c

tel que P(l) < 0

et donc si tu en étudies le signe tu auras la réponse au problème ; )

[Axel0293]

On a :

2(l+L) = 80 (1)
l*L > 384 (2)

(1) => L = 40-l

donc dans (2) : l*(40-l) > 384

Et tu peux mettre ça sous la forme d'un polynôme du second degré P(l) = a*l^2 +b*l + c

tel que P(l) < 0

et donc si tu en étudies le signe tu auras la réponse au problème ; )

Merci beaucoup pour tes explications précises je cerne mieux l'exercice à présent