Equation complexe 3eme degré
15 messages
- Page 1 sur 1
Equation complexe 3eme degré
Bonjour,
Je bloque sur la résolution de l'équation suivante:
z^3 = -1 + i
Quelqu'un peut il m'aider svp? rien qu'une toute petite piste? :)
Un grand merci par avance!
Je bloque sur la résolution de l'équation suivante:
z^3 = -1 + i
Quelqu'un peut il m'aider svp? rien qu'une toute petite piste? :)
Un grand merci par avance!
Salut !
Pour résoudre cette équation, on va étudier séparément le module et l'argument.
Pour ça, on prend sous forme trigonométrique en posant
sous forme trigonométrique en posant 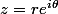 avec
avec 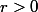 (
( est le module de
est le module de  ) et
) et  (
( est l'argument de
est l'argument de  ).
).
Ecris alors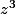 et
et 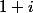 sous forme trigonométrique.
sous forme trigonométrique.
Du coup, si et seulement si
si et seulement si 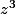 et
et 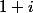 ont même module et
ont même module et 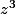 et
et 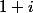 ont même argument (modulo
ont même argument (modulo  )
)
Camille05 a écrit:Bonjour,
Je bloque sur la résolution de l'équation suivante:
z^3 = -1 + i
Quelqu'un peut il m'aider svp? rien qu'une toute petite piste?
Un grand merci par avance!
Pour résoudre cette équation, on va étudier séparément le module et l'argument.
Pour ça, on prend
Ecris alors
Du coup,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Camille05 a écrit:Ah oui oui dsl, je suis à coté de la plaque.. Donc c'est bien la même méthode que capitaine nuggets !
Mais il reste toujours la question du "qu'est ce que je fais du degré 3 de z" ?
Généralité ... à retenir :
z^n = r * e^(i. (theta + 2k.Pi))
|z^n| = r
arg(z^n) = theta + 2k.Pi
*****
et aussi : |z| = (|z^n|)^(1/n)
arg(z) = (1/n).arg(z^n)
*****
Ici, n = 3 et |z^n| = |z³| = V2 et arg(z^n) = arg(z³) = 3Pi/4 + 2k.Pi
Tu peux donc avec ce qui précède calculer |z| et arg(z)
Les 3 solutions pour arg(z) se trouvent en prenant k = 0, 1 et 2
:zen:
Coucou
On a posé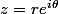 où
où 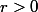 et
et 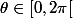
- Ecrivons alors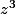 sous forme trigonométrique en fonction de la forme trigonométrique
sous forme trigonométrique en fonction de la forme trigonométrique 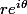 de
de  :
:
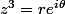^3 = r^3 e^{i(3\theta)}=r' e^{i\theta '}) en posant respectivement
en posant respectivement  et
et  .
.
- Ecrivons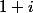 sous forme trigonométrique :
sous forme trigonométrique :  .
.
- Connaissant les forme trigonométrique de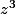 et
et 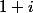 , on a :
, on a :
[CENTER] [/CENTER]
[/CENTER]
En trouvant alors et
et  , tu trouveras les complexes z solutions de ton équation :++:
, tu trouveras les complexes z solutions de ton équation :++:
capitaine nuggets a écrit:Salut !
Pour résoudre cette équation, on va étudier séparément le module et l'argument.
Pour ça, on prendsous forme trigonométrique en posant
avec
(
est le module de
) et
(
est l'argument de
).
Ecris alorset
sous forme trigonométrique.
Du coup,si et seulement si
et
ont même module et
et
ont même argument (modulo
)
On a posé
- Ecrivons alors
- Ecrivons
- Connaissant les forme trigonométrique de
[CENTER]
En trouvant alors
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
chan79 a écrit:Salut
C'est bizarre ...
Ouais, j'ai oublier le signe moins devant le "1" ...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Camille05 a écrit:Bonjour,
Merci à tous pour votre aide, je n'ai malheureusement pas réussi à terminer mon devoir à temps malgré votre aide.
J'ai eu la correction, et cétait sur la bonne voie. Il faut utiliser le théorème d'Alembert.
Merci encore
J'ai un peu de mal à comprendre comment tu n'avais pas abouti avec l'aide reçue.
-1+i = V2.(-1/V2 + i.1/V2) = V2.e^(i.(3Pi/4 + 2k.Pi))
z³ = V2.e^(i.(3Pi/4 + 2k.Pi))
Les 3 solutions se trouvent en attribuant à k les valeurs 0, 1 , 2
Ou si on préfère:
:zen:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
