Fonction du 2nd degré

[Cloados]

Bonjour, j'ai un exercice de maths que je ne comprends pas pouvez-vous m'expliquer ?
Une personne dispose de 40 mètres de clôtures. a l'aide de cette clôture, elle délimite un enclos RECTANGULAIRE en s'appuyant contre un mur rectiligne. L'objectif de l'exercice est de déterminer les dimensions de l'enclos pour obtenir l'aire maximal.
On suppose que la longueur du mur est supérieur a 40 mètres.
On note x et L les dimensions de l'enclos. (x largeur, L longueur)
1) sachant que la longueur de la clôture est de 40 mètres, écrire une relation entre x et L
En déduire L en fonction de x puis déterminer l'aire f(x) de l'enclos en fonction de x
Justifier que la fonction f est définie sur l'intervalle [0;20]
Vérifier que g(x)= -2(x-10)²+200
2) Établir un tableau de variation de la fonction f définie sur l'intervalle [0;20] puis conclure.

1) On suppose que la longueur du mur est égale a 10 mètres.
quel est l'aire de l'enclos si le mur correspond exactement à un coté de l'enclos
2) on suppose maintenant que le mur ne correspond qu'a une parti du coté de l'enclos, on note comme précédemment x et L, les dimensions de l'enclos.
a) déterminer L en fonction de x puis l'aire g(x) de l'enclos en fonctions de x
Justifier que la fonction g est définie sur l'intervalle [0;15]
Vérifier que g(x)= -(x-12,5)² + 156,25
b) établir le tableau de variation de la fonction g(x)

par avance merci beaucoup

[tototo]

[quote="Cloados"]Bonjour, j'ai un exercice de maths que je ne comprends pas pouvez-vous m'expliquer ?
Une personne dispose de 40 mètres de clôtures. a l'aide de cette clôture, elle délimite un enclos RECTANGULAIRE en s'appuyant contre un mur rectiligne. L'objectif de l'exercice est de déterminer les dimensions de l'enclos pour obtenir l'aire maximal.
On suppose que la longueur du mur est supérieur a 40 mètres.
On note x et L les dimensions de l'enclos. (x largeur, L longueur)
1) sachant que la longueur de la clôture est de 40 mètres, écrire une relation entre x et L
L+2x=40
En déduire L en fonction de x puis déterminer l'aire f(x) de l'enclos en fonction de x
Justifier que la fonction f est définie sur l'intervalle [0;20]
Vérifier que g(x)= -2(x-10)²+200
2) Établir un tableau de variation de la fonction f définie sur l'intervalle [0;20] puis conclure.

1) On suppose que la longueur du mur est égale a 10 mètres.
quel est l'aire de l'enclos si le mur correspond exactement à un coté de l'enclos
2) on suppose maintenant que le mur ne correspond qu'a une parti du coté de l'enclos, on note comme précédemment x et L, les dimensions de l'enclos.
a) déterminer L en fonction de x puis l'aire g(x) de l'enclos en fonctions de x
Justifier que la fonction g est définie sur l'intervalle [0;15]
Vérifier que g(x)= -(x-12,5)² + 156,25
b) établir le tableau de variation de la fonction g(x)

par avance merci beaucoup

[Cloados]

Merci mais L en fonction de x ? comment faire ?

[LaCoc6nl]

Le périmètre de l'enclos: et l'aire de l'enclos: sont positifs.
La définition de , absente, est à rajouter: est-ce la dérivée de ? L'indice des questions est à revoir...

[jlq]

Le périmètre de l'enclos: et l'aire de l'enclos: sont positifs.
La définition de , absente, est à rajouter: est-ce la dérivée de ? L'indice des questions est à revoir...

Attention comme on s'appuie sur un mur je pense L+2x=40

[spike0789]

Salut,

Oui en effet L+2x=40
et g=f (erreur de frappe je pense)

[LaCoc6nl]

Si le mur sert comme côté de l'enclos, la longueur de corde L et une largeur de 2x font le tour à 40.
(on peut aussi dans une lecture optimale interprétée maintenir un écart entre mur et enclos fermé).
. Si le mur correspond à un côté de l'enclos (L=10), . L'aire f(x) de l'enclos est constante.
Si le mur ne correspond qu'à une partie du côté de l'enclos à définir, il faut avoir :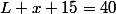 pour que l'expression de f soit vérifiée ce qui indique la donnée du lien entre x et la fraction du côté identifiée absente de l'énoncé. En effet, ici, à moins d'une erreur additionnelle sur l'expression de f: .