Fonction exponentielle

[argalon]

Bonjour, mon prof m'a demandé de faire l’étude de la fonction f(x) = 13-13e^-0.5x en trois étapes

a.Calculer la fonction dérivée f'(x) de f(x).
b.Faire l'étude du signe de f'(x) sur l'intervalle [0;15].
c.Tracer le tableau de variation sur cet intervalle.

J'ai cherché sur internet mais je n'est pas trouvé d’étude semblable sur les fonctions exponentielles
Merci de bien vouloir m'aider et surtout de m'expliquer comment faire l’étude d'une fonction exponentielle :lol3:

[chan79]

Bonjour, mon prof m'a demandé de faire l’étude de la fonction f(x) = 13-13e^-0.5x en trois étapes

a.Calculer la fonction dérivée f'(x) de f(x).
b.Faire l'étude du signe de f'(x) sur l'intervalle [0;15].
c.Tracer le tableau de variation sur cet intervalle.

J'ai cherché sur internet mais je n'est pas trouvé d’étude semblable sur les fonctions exponentielles
Merci de bien vouloir m'aider et surtout de m'expliquer comment faire l’étude d'une fonction exponentielle :lol3:

salut
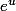
la dérivée de est

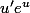
[argalon]

Donc sa dérivée serait -0.5e^-0.5x ?
Vu que 13 et -13 sont des constantes non ??
Je ne suis pas du tout sure de moi dites moi si je me trompe...

[Archibald]

Bonjour,

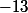
13 est bien une constante mais est un coefficient de ta fonction exponentielle. Et tu sais que : d'où

[argalon]

Donc se serait -13.e^-0.5x ?
si dans t'on expression K est le coefficient directeur
mais quesque je fais de la dérivée de e^U ? je la laisse comme sa ?

[Archibald]

Ben non tu la dérives, mais qu'une fonction soit multipliée ou divisée par une constante , lorsque tu la dérives tu ne touches pas à .



Si tu veux t'en convaincre, pose et essaye de dériver

[argalon]

je ne comprend pas trop j'aurais besoin d'un exemple concret et détailler svp

[Archibald]

Soit . Tu vas dériver cette fonction en la considérant comme le produit de deux fonction : et

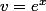
Tu sais dériver un produit, n'est-ce pas ?

[argalon]

Ben oui c'est facile tu te sert de U.V et tu fait u'.v + u.v' donc :
U= 5 U'=0
v=e^x v'=e^x
f=U.V
f'=U'.V+V'.U
f'(x)=0.e^x+e^x.5
f'(x)=e^x.5
c'est pas sa ??

[Archibald]

Si c'est bien ça. Et donc tu remarques bien que la dérivée de est

[argalon]

Ouai, ouai ok , mais ce qui me pose problème dans mon énoncer f(x) = 13-13e^-0.5x
c'est que je ne sais pas quoi faire de 13 et -13
es-que je dois supprimer le premier treize comment dois-je les calculer avec l’exponentielle ??

[Archibald]

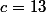
Ta fonction est une somme d'une constante et d'une fonction exponentielle multipliée par une autre constante .

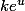
Quelle est la dérivée de la constante ? quelle est la dérivée de ? (lis ce qui a été écrit plus haut)

[argalon]

Si je suis t'on raisonnement en appliquant k.e^U, je dois donc faire la dérivée de e^U sans toucher à K ?
Sa donnerait cela: -13-0.5e^-0.5x
en éliminent la première constante bien entendu...

[argalon]

Tu peux m'aider s'il te plait ??

[Archibald]

Mis à part que c'est (-13) FOIS (-0,5)e^(-0,5x), ta réponse est correcte.

je dois donc faire la dérivée de e^U sans toucher à K

OUI. Une dernière fois : (u +/- k)' = u' MAIS (k x u)' = k x u'