Bonsoir à tous,
j'ai un problème dans un exercice, je n'arrive pas à déterminer la matrice de passage d'une base à une autre.
Voici l'énoncé de l'exo :
J'ai trois vecteurs
1- Montrer qu'ils forment une base de R3. C'est fait!
Écrire la matrice de passage de la base canonique B à cette base B'. Calculer P-1.
Je comprends pas comment tout d'abord trouver la base canonique ?? :marteau:
Si ça peut aider les vecteurs sont (1,-1,0) (1,1,1) et (0,1,1). Mais l'application numérique n'est pas le plus important, j'aimerais bien comprendre... J'ai parcouru plusieurs forum et sites, en vain.....
En vous remerciant.
Matrice de passage
9 messages
- Page 1 sur 1
Ihaveadream a écrit:Bonsoir à tous,
j'ai un problème dans un exercice, je n'arrive pas à déterminer la matrice de passage d'une base à une autre.
Voici l'énoncé de l'exo :
J'ai trois vecteurs
1- Montrer qu'ils forment une base de R3. C'est fait!
Écrire la matrice de passage de la base canonique B à cette base B'. Calculer P-1.
Je comprends pas comment tout d'abord trouver la base canonique ?? :marteau:
Si ça peut aider les vecteurs sont (1,-1,0) (1,1,1) et (0,1,1). Mais l'application numérique n'est pas le plus important, j'aimerais bien comprendre... J'ai parcouru plusieurs forum et sites, en vain.....
En vous remerciant.
Salut,
La base canonique de R^3 est simplement B=((1,0,0), (0,1,0), (0,0,1))
Kikoo <3 Bieber a écrit:Salut,
La base canonique de R^3 est simplement B=((1,0,0), (0,1,0), (0,0,1))
Merci beaucoup !! Donc à chaque fois que l'on me parle de base canonique, elle est spécifique à R^n c'est bien ça ?
Et pour la matrice de passage, je dois trouver une relation entre chaque vecteur de chaque base c'est bien ça ? par exp mon premier vecteur avec (1,0,0) etc...?
Base canonique de 
On a donc un espace de départ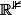 muni de sa base canonique
muni de sa base canonique )
On découvre une nouvelle base de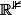 :
: 

Et on désire donc sa matrice de passage =
= ) On vérifie aisément que :
On vérifie aisément que :



D'où :

Et pour calculer , disons que tu fais le chemin inverse. Là, c'est assez trivial puisqu'on te donne la base canonique comme base initiale.
, disons que tu fais le chemin inverse. Là, c'est assez trivial puisqu'on te donne la base canonique comme base initiale.
On a donc un espace de départ
On découvre une nouvelle base de
Et on désire donc sa matrice de passage
D'où :
Et pour calculer
Archibald a écrit:Tout à fait. C'était pour savoir si tu suivais
:lol3: Ahah
Dernière question, comment fait-on pour déterminer une matrice d'une application linéaire dans une base ? (ici en loccurrence il s'agit de ma base b')
J'arrive à le faire dans la base cano, mais dans une base en particulier... :hein:
Hum, je n'ai pas vraiment le temps mais voici un lien qui devrait faire l'affaire (l'explication commence à la proposition 6)
http://ljk.imag.fr/membres/Bernard.Ycart/mel/cm/node5.html
http://ljk.imag.fr/membres/Bernard.Ycart/mel/cm/node5.html
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
