Aide Math Seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 13:41
par Margaux13 » 25 Avr 2013, 13:41
bonjour bonjour,
alors voilà j'ai cet exercice

Le problème c'est que je ne vois pas comment calculer les coordonnées de A B ou C car on a aucun nombre, fin d'habitude on a par exemple P (xp;yp) la rien du tout, j'espère vous allez pourvoir m'aider. Merci d'avance

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 13:52
par ampholyte » 25 Avr 2013, 13:52
Bonjour,
Le petit piège est que tu ne trouves pas dans le repère (O; i; j) habituel mais dans le repère
)
Ici A est donc l'origine, le vecteur

définit donc l'axe des abscisses et

définit l'axe des ordonnées. Ces vecteurs sont unitaires ! donc ...
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 13:57
par Margaux13 » 25 Avr 2013, 13:57
ampholyte a écrit:Bonjour,
Le petit piège est que tu ne trouves pas dans le repère (O; i; j) habituel mais dans le repère
)
Ici A est donc l'origine, le vecteur

définit donc l'axe des abscisses et

définit l'axe des ordonnées. Ces vecteurs sont unitaires ! donc ...
ah merci je crois avoir compris
donc A (0;0)
B ( 1;0)
C (0;1) ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 13:59
par ampholyte » 25 Avr 2013, 13:59
Margaux13 a écrit:ah merci je crois avoir compris
donc A (0;0)
B ( 1;0)
C (0;1) ?
C'est tout à fait ça

.
Petite précision, les axes du repère ne sont pas forcéments orthogonaux !
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 14:40
par Margaux13 » 25 Avr 2013, 14:40
ampholyte a écrit:C'est tout à fait ça

.
Petite précision, les axes du repère ne sont pas forcéments orthogonaux !
Je voudrais pas abuser de votre gentillesse mais est ce que c'est bon ? E(1;0,5)
D(0,5;1)
I(0,75;0,75)

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 14:57
par ampholyte » 25 Avr 2013, 14:57
C'est tout bon =).
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 15:08
par Margaux13 » 25 Avr 2013, 15:08
ampholyte a écrit:C'est tout bon =).
Ah merci

-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 15:25
par Margaux13 » 25 Avr 2013, 15:25
Par contre est ce que vous pouvez m'aider pour la Q4 s'il vous plait?
parce que j'ai trouver G(1,25;1,25) mais je pense que c'est faux..

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 15:49
par ampholyte » 25 Avr 2013, 15:49
Je trouve G(-1/4, -1/4) de mon côté
En abscisse :
6(0 - xg) - (1 - xg) - (0 - xg) = 0
-6xg - 1 + xg + xg = 0
-4xg = 1
xg = -1/4
En ordonnée
6(0 - yg) - (0 - yg) - (1 - yg) = 0
-6yg + yg - 1 + yg = 0
-4yg = 1
yg = -1/4
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 16:10
par Margaux13 » 25 Avr 2013, 16:10
ampholyte a écrit:Je trouve G(-1/4, -1/4) de mon côté
En abscisse :
6(0 - xg) - (1 - xg) - (0 - xg) = 0
-6xg - 1 + xg + xg = 0
-4xg = 1
xg = -1/4
En ordonnée
6(0 - yg) - (0 - yg) - (1 - yg) = 0
-6yg + yg - 1 + yg = 0
-4yg = 1
yg = -1/4
Par contre pour après ca ne marche pas, pour prouver qu'il est parallèlogramme il faut calculer le milieu des diagonales (DE) et (GI) pour voir si ils sont identiques. Mais la ca ne marche pas, ca marcherais si g(1/4;1/4) tu comprends ce que je veux dire? :/

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 16:16
par ampholyte » 25 Avr 2013, 16:16
edit : coquille
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 16:24
par Margaux13 » 25 Avr 2013, 16:24
ampholyte a écrit:Revoie tes calculs :
Méthode 1 :
GB (3/4, -1/4)
IC (3/4, -1/4)
GB et IC sont colinéaires donc GBIC est un parallélogramme.
Méthode 2 :
Soit H le milieu de GI alors H a pour coordonnée :
H ((xg + xi)/2, (yg + yi)/2) = (1/2, 1/2)
Soit M le milieu de BC alors M a pour coordonnée :
M ((xb + xc)/2, (yb + yc)/2) = (1/2, 1/2)
M et H sont confondues dont les diagonales se coupent en leur milieu donc GBIC est un parallélogramme.
j'ai ca sauf que je trouve (xg+xi)/2 (-0.25+0.75)= 0,5/2=0.25 pareil pour y.
je vois pas où est mon erreur en fait :/

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 16:26
par ampholyte » 25 Avr 2013, 16:26
Margaux13 a écrit:j'ai ca sauf que je trouve (xg+xi)/2 (-0.25+0.75)= 0,5/2=0.25 pareil pour y.
je vois pas où est mon erreur en fait :/
Hop désolé petite coquille de ma part. Je regarde ce qui cloche pour le calcul des diagonales.
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 16:29
par Margaux13 » 25 Avr 2013, 16:29
ampholyte a écrit:Hop désolé petite coquille de ma part. Je regarde ce qui cloche pour le calcul des diagonales.
C'est pas grave c'est déjà gentille de m'aider


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Avr 2013, 16:45
par ampholyte » 25 Avr 2013, 16:45
Bon alors reprenons différemment le calcul :
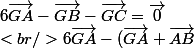 - (\vec{GA} + \vec{AC}) = \vec{0} \\<br /><br />4\vec{GA} - \vec{AB} - \vec{AC} = \vec{0} \\<br /><br />\vec{GA} = \frac{\vec{AB} + \vec{AC}}{4})



Je trouve toujours G(-1/4, -1/4).
Même en plaçant le point G directement sur la figure, je tombe sur G(-1/4, -1/4), il y a peut-être une petite erreur dans l'énoncé, ou alors je ne vois pas mon erreur =).
Si l'équation à résoudre était :

cela fonctionnerait.
-
Margaux13
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Déc 2012, 16:03
-
 par Margaux13 » 25 Avr 2013, 16:53
par Margaux13 » 25 Avr 2013, 16:53
ampholyte a écrit:Bon alors reprenons différemment le calcul :
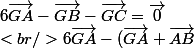 - (\vec{GA} + \vec{AC}) = \vec{0} \\<br /><br />4\vec{GA} - \vec{AB} - \vec{AC} = \vec{0} \\<br /><br />\vec{GA} = \frac{\vec{AB} + \vec{AC}}{4})



Je trouve toujours G(-1/4, -1/4).
Même en plaçant le point G directement sur la figure, je tombe sur G(-1/4, -1/4), il y a peut-être une petite erreur dans l'énoncé, ou alors je ne vois pas mon erreur =).
Si l'équation à résoudre était :

cela fonctionnerait.
oui c'est bon moi aussi je trouve ça

faudrais peut etre que je revoit mes calculs pour i alors

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités


définit donc l'axe des abscisses et
définit l'axe des ordonnées. Ces vecteurs sont unitaires ! donc ...

