Suites géométriques 1ère S

[Cristys17]

J'ai une exercice que je n'arrive pas à comprendre. Enfin je n'arrive pas bien a savoir comment je dois le prouver. Même je sais que c'est juste.

Montrer que pour tout entier n naturel, 2 + 2/3 + 2/9 +...+ 2/3^n = 3 - 1/3^n.

J'ai essayé de faire la formule des deux. Mais ça ne prouve rien du tout.
Pour la 1, v0=2 et q=3

[siger]

J'ai une exercice que je n'arrive pas à comprendre. Enfin je n'arrive pas bien a savoir comment je dois le prouver. Même je sais que c'est juste.

Montrer que pour tout entier n naturel, 2 + 2/3 + 2/9 +...+ 2/3^n = 3 - 1/3^n.

J'ai essayé de faire la formule des deux. Mais ça ne prouve rien du tout.
Pour la 1, v0=2 et q=3

Pourrais-tu etre plus clair:de quoi parles-tu exactement?
"la formule des deux" ?
"Pour la 1, v0=2 et q=3" ?
....

[Cristys17]

Alors la question du sujet est poser comme cela. Et j'ai essayé de trouver les V0 des deux et leur raison mais elles ne sont pas pareils. Je parlais de la branche gauche de l'expression.

[siger]

Mille excuses : fausse manip = effacement!

On peut ecrire
2 + 2/3 + 2/9 +...+ 2/3^n = 2( 1 + 1/3 + 1/3² + .. 1/3¨n)
le terme entre parentheses est la somme d'une progression geometrique de raison r=1/3 et de premier terme a=1
a + ar + ar² + .... +ar^n = a(1-r^(n+1))/(1-r)
d'ou ......

[capitaine nuggets]

Salut !

En factorisant le membre de gauche par , on a :
.
Or étant la somme de 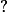termes consécutifs d'une suite géométrique de premier terme 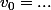et de raison 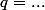, tu en déduis que :
.
D'où .


:+++:

[Cristys17]

D'où 1/3 + 1/3^2 +...+ 1/3^n = (1/(1/3^(n+1/3)/1-1/3 ?? C'est cela?

[siger]

Ton ecriture est tout sauf claire....

Tu connais la reponse somme = 3-1/3^n
reponse que tu trouveras si tu appliques correctement le resultat qui t'as été indiqué.