raolivi a écrit:merci singer .
Bon je n'est jamais appris les eq du cercle (ou je ne m'en souviens plus )
j'ai donc fait un graph pour mieux comprendre et je commence a comprendre votre démarche .
avant de continuer j'aimerais bien comprendre un peu plus et comment trouvez vous l'eq de la corde ?
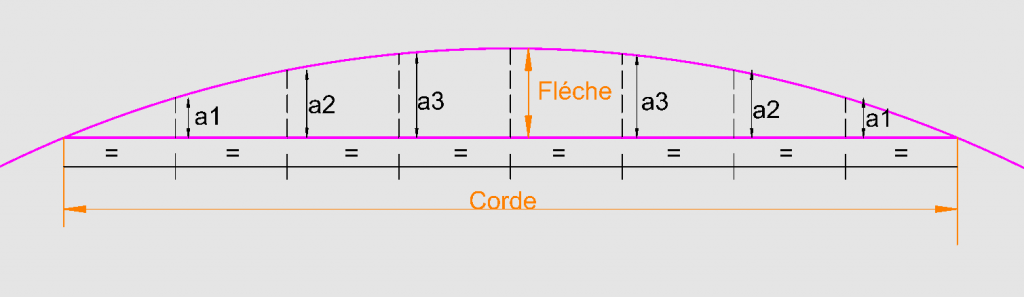
dans mon exemple la corde a comme coordonnées [0;0 ] à [1;0] .
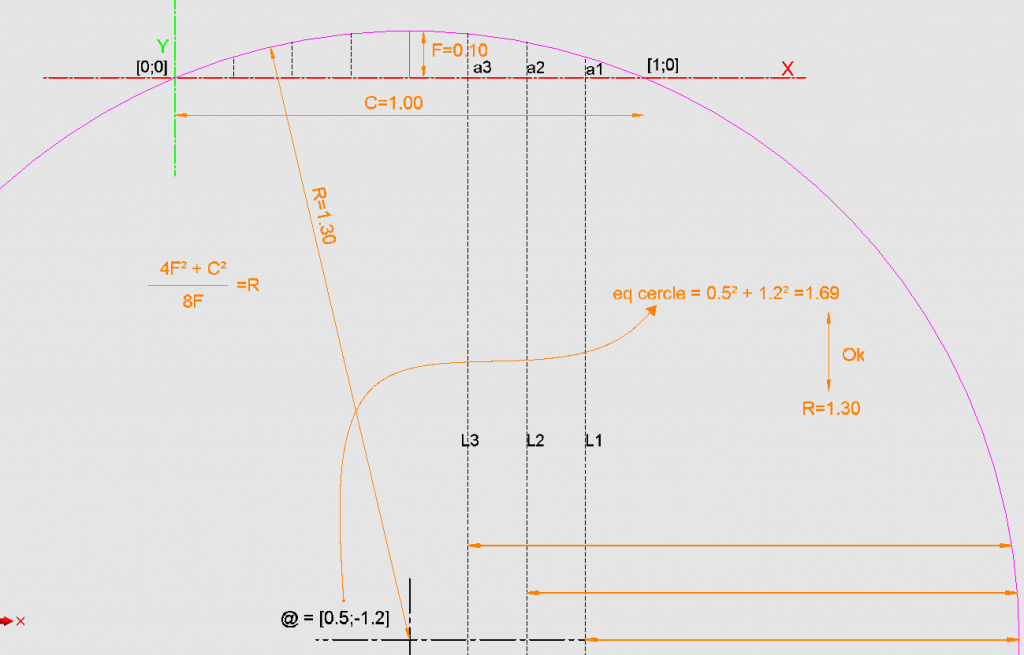
avec l'eq du cercle et en mode graphique j'ai effectivement trouvé la valeur du rayon et j'ai comparer avec la formule 4F² + c² etc.. ça marche , j'ai donc mon rayon de connu .
maintenant comment trouver avec F (Flèche) et r (rayon) les coordonnées de la cordes , ou comment le démontrer ? avec ça je comprendrais mieux pour trouver le reste .
votre formule : "- l'équation de la corde : y= (R-h)"
merci .
bien pas bien compris votre
Re
soit O le centre du cercle, A une intersection du cercle et de le corde B le sommet de la fleche et C l'intersection de la corde et de OB
on a CB = f et CA = c/2
le triangle OAC est rectangle et l'on a R^2=(R-f)^2 + (c/2)^2 d'ou R = (( c/2)^2+ f^2 )/2f
l'equation du cercle de centre O ( dans le systeme d'axes (O,x,OB=y) est
x^2+ y^2= R^2
la corde est a l'ordonnee Yc = R -f
par suite les coordonnees du point sur le cercle, correspodant a a3 ( premiere division a partir du centre) sont
X = c/ 8
Y = racine( R^2 - c^2/64) et la longueur de la fleche au niveau a3 est egale a Y -Yc
...
idem pour a2 avec x = c/4
...'.
j'espere avoir ete assez clair, car je n'ai pas pour l'instant les moyens de realiser un dessin!