Bonjour, je bloque depuis quelques jours déjà sur le problème suivant:
"Dans un récipient de forme cylindrique, de rayon 4cm, on verse de l'eau jusqu'à une hauteur de 3,75cm. On veut alors placer une bille dans le récipient de façon a ce que le liquide la recouvre exactement. Déterminer le rayon de la bille.
1) Mettre en équation ce problème ( faire un schéma donner des noms aux inconnues, et simplifier au max)."
J'en ai conclu que la hauteur d'eau était maintenant donc égale à 3,75+x (elle a augmentée lorsqu'on a rajouté la bille) et que donc le volume de la boule (4/3*pi*r*r*r) était égal (on fait comme si la boule était de l'eau que l'on a versé qui forme donc maintenant un cylindre (pi*4*4*hauteur ou x
J'ai donc le début : 4/3*pi*r*r*r=pi*16*x
De plus j'ai eu l'aide d'un ami qui m'a dit que l'équation final que je devrai trouver est "rayon de la boule=(r*r+45)/24
A partir de ce moment je n'y arrive plus, pouvez vous m'aider a trouver l'étape qui me manque pour parvenir à l'équation final? Merci d'avance a ce qui pourront m'aider. (ps: je suis au niveau seconde)
Volumes
3 messages
- Page 1 sur 1
Je ne comprends rien à ton explication xDxD.
Soit x l'augmentation de la hauteur après l'ajout de la bille.
Soit r le rayon de la bille.
A partir de là, il faut que tu trouves des équations :
1] "de façon a ce que le liquide la recouvre exactement" =>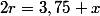
2] Égalisons maintenant les volumes :
V_{cylindre de h = 3,75} + V_{boule de rayon r} = V_{cylindre de h = 3,75 + x}
*16*\pi)
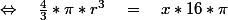
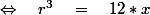
 \quad = \quad 0)

Indice : 3 est racine de ce polynôme. (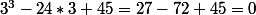 )
)
Soit x l'augmentation de la hauteur après l'ajout de la bille.
Soit r le rayon de la bille.
A partir de là, il faut que tu trouves des équations :
1] "de façon a ce que le liquide la recouvre exactement" =>
2] Égalisons maintenant les volumes :
V_{cylindre de h = 3,75} + V_{boule de rayon r} = V_{cylindre de h = 3,75 + x}
Indice : 3 est racine de ce polynôme. (
Cheche a écrit:Je ne comprends rien à ton explication xDxD.
Soit x l'augmentation de la hauteur après l'ajout de la bille.
Soit r le rayon de la bille.
A partir de là, il faut que tu trouves des équations :
1] "de façon a ce que le liquide la recouvre exactement" => 2r = 3,75 + x
2] Égalisons maintenant les volumes :
V_{cylindre de h = 3,75} + V_{boule de rayon r} = V_{cylindre de h = 3,75 + x}
Indice : 3 est racine de ce polynôme. ()
Merci beaucoup beaucoup! Désolé si mon explication n'était pas clair, c'est parfois difficile de mettre à l'écrit ce qu'on a dans la tête
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
