Une intégrale un peu exotique

[egan]

Salut tout le monde,

Est-ce que quelqu'un connait une méthode pour calculer cette intégrale ?



Merci d'avance.

@+ Boris.

[Pianoo]

Est-ce que quelqu'un connait une méthode pour calculer cette intégrale ?

[EDIT]Nan mais après ça coince de toute façon :hum:

Je n'ai pas fait le calcul jusqu'au bout ... Mais par changement de variables j'arrive à :


(ça j'ai vérifié sur un calculateur)

Ensuite tu peux faire une intégration par partie :
u'v avec
qui s'intégre bien
et qui se dérive ................ avec du courage :dodo:

[Mathusalem]

Tu peux récrire ton intégrand comme ceci

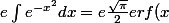, avec erf(x) la fonction erreur qui est définie comme la primitive de la gaussienne. Quand tu évalues entre -1 et 1, ça donne ~4.06

[Joker62]

Il me semble que soit l'argument de l'exponentielle.

[Pythales]

Les bornes -1 et +1 devraient inciter à poser ...

[adrien69]

Si l'on regarde bien, tout le poids de l'intégrande est en 0, donc on peut penser à développer en série entière en 0.
Et le développement est donné par la suite (an/n!) où (an) est la suite A000262 de l'OEIS. Ça te donne un moyen de calculer numériquement l'intégrale jusqu'à la précision que tu souhaites. Voilà voilà ! http://oeis.org/A000262

[JeanJ]

Bonjour,

cette intégrale ne peut pas s'exprimer avec un nombre fini de fonctions élémentaires. Si l'on veut une expression litérale qui ne soit pas sous forme de série infinie, il faut faire appel à une fonction spéciale, la fonction de Tricomi (ou fonction confluente hypergéométrique de seconde espèce).
Les valeurs numériques de cette fonction se trouvent dans des tables, ou plus précisément sont données par les logiciels mathématiques (WolframAlpha par exemple)
On peut arriver assez rapidement à la solution en se ramenant à une transformée de Laplace connue (page jointe)

Désolé, il ne semble pas possible de joindre un document. Si vous êtes intéressé, contactez moi par la messagerie personnelle du site pour que je puisse vous envoyez cette page.