Bonjour,
Mon problème est le suivant :
Soit E un espace de fonctions (définies sur R et à valeurs, par exemple, complexes) muni d'une norme N. L'espace n'est PAS suposé complet.
Soient Fn une suite d'éléments de E telle que
1) La série des Fn converge normalement sur R vers une fonction F, élément de E.
2) La série des normes N(Fn) est convergente.
A-t-on l'inégalité N(F) <= Sum(N(Fn)) ?
Dans les faits E est un sous-espace de l'ensemble des fonctions 2*Pi périodiques et indéfiniment dérivables, mais je ne sais pas si cette hypothèse est utile.
Cette question m'est inspiré par les questions 4.3 et 4.4 de la deuxième partie d'ULM-Cachan 2004. Le correcteur (sur le site de l'UPS) parle d'une "...généralisation de l'inégalité triangulaire..." J'ai l'impression que quelque chose m'echappe totalement !
Merci d'avance pour ceux qui ont des idées (ou qui veulent se donner la peine de regarder directement l'énoncé de l'épreuve..) !
Cordialement
Espace fonctionel - Série de fonction et norme
13 messages
- Page 1 sur 1
Bonjour,
Oui l'inégalité et vraie.
Par généralisation de l'inégalité triangulaire le correcteur veut dite avec une somme de p termes au lieu de 2 seulement :
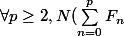\leq \sum_{n=0}^pN(F_n))
qui se montre très bien par récurrence sur p.
Une fois que tu as ça, c'est presque fini : le terme de gauche tend vers N(F) (A montrer avec l'autre inégalité triangulaire classique), quand au terme de droite converge par définition vers la somme de ta série.
Damien
Oui l'inégalité et vraie.
Par généralisation de l'inégalité triangulaire le correcteur veut dite avec une somme de p termes au lieu de 2 seulement :
qui se montre très bien par récurrence sur p.
Une fois que tu as ça, c'est presque fini : le terme de gauche tend vers N(F) (A montrer avec l'autre inégalité triangulaire classique), quand au terme de droite converge par définition vers la somme de ta série.
Damien
je tente mais je ne garantie riendelnico a écrit:Bonjour,
Mon problème est le suivant :
Soit E un espace de fonctions (définies sur R et à valeurs, par exemple, complexes) muni d'une norme N. L'espace n'est PAS suposé complet.
Soient Fn une suite d'éléments de E telle que
1) La série des Fn converge normalement sur R vers une fonction F, élément de E.
2) La série des normes N(Fn) est convergente.
A-t-on l'inégalité N(F) <= Sum(N(Fn)) ?
Dans les faits E est un sous-espace de l'ensemble des fonctions 2*Pi périodiques et indéfiniment dérivables, mais je ne sais pas si cette hypothèse est utile.
Cette question m'est inspiré par les questions 4.3 et 4.4 de la deuxième partie d'ULM-Cachan 2004. Le correcteur (sur le site de l'UPS) parle d'une "...généralisation de l'inégalité triangulaire..." J'ai l'impression que quelque chose m'echappe totalement !
Merci d'avance pour ceux qui ont des idées (ou qui veulent se donner la peine de regarder directement l'énoncé de l'épreuve..) !
Cordialement
pour k entier N(F) =N[F - somme((jusqueàk)Fn) + somme((jusqu'àk)Fn)]
N norme donc c'est inférieur ou égal à N[F-somme((jusquàk)Fn)] + somme(jusquàk)N[Fn]
la série à terme positif N[Fn] converge donc on majore par sa somme; il vient
pour tout k entier N[F]<= N[F-somme((jusquàk)(Fn))] + sommeN[Fn]
la convergence normale de Fn vers F donne le résultat
qu'en penses-tu?
DamX a écrit:Bonjour,
Oui l'inégalité et vraie.
Par généralisation de l'inégalité triangulaire le correcteur veut dite avec une somme de p termes au lieu de 2 seulement :
qui se montre très bien par récurrence sur p.
Une fois que tu as ça, c'est presque fini : le terme de gauche tend vers N(F) (A montrer avec l'autre inégalité triangulaire classique), quand au terme de droite converge par définition vers la somme de ta série.
Damien
Damien,
Le coeur de ma question est bien là : pourquoi le membre de gauche tend vers N(F) ?? Peut-être me suis-je mal exprimé mais quand je dis qu'il y a convergence normale sur R c'est au sens de la norme infini classique (valeur absolue), donc à priori, la série ne converge pas DANS E (au sens de N).
Comment dès lors peut-on passer à la limite dans N(Sum(Fn)) ?
C'est précisément ça qui m'échappe !
Merci d'avance !
Doraki a écrit:Donc tu supposes que la somme des Fn converge vers F pour la norme infinie, que la somme des N(Fn) converge dans R, et tu veux montrer que Fn converge vers F pour la norme N ?
Oui pour les hypothèses : la somme des Fn converge pour la norme infinie (il y a même convergence normale de la série pour la norme infinie) vers F élément de E, et la somme des N(Fn) converge dans R.
Si on arrive effectivement à montrer que que la somme des Fn converge vers F pour la norme N le problème est résolu.
Mais je ne vois pas comment on peut affirmer une telle chose, et de plus E n'est pas supposé complet...
Doraki a écrit:Si N est vraiment une norme quelconque, je suis quasi-convaincu que c'est faux, mais je vois pas de contre-exemple.
C'est ce que je pense aussi, même si la norme en fait n'est pas quelconque...
Si tu as le courage de regarder ULM Cachan 2004 : dans la partie 1 les questions 1 à 7 sont inutiles et peuvent être juste parcourues, seule la question 8.4 est utile ; dans la partie 2 les questions 1 et 2 ne présentent aucune difficulté; reste donc 3 (là aussi auncun souci) et enfin 4 pour arriver à 4.3 et 4.4 (qui sont en fait similaires).
La correction de ces questions fait 5 lignes avec un passage à la limite à mon sens injustifié dans une situation qui est celle de mon post.
J'ai réussi à contacter le correcteur (il y a plein de corrections de lui d'ailleurs sur le site de l'UPS) : même s'il a reconnu être allé un peu vite il m'a simplement dit que "....la convergence normale réglait le problème...". J'ai bien vu qu'il avait la flemme de se replonger dans ce vieux problème, ce que je peux comprendre bien sûr. En même temps il était prof de spécial donc il doit savoir ce qu'il dit, et donc quelque chose m'echappe et j'aimerais bien savoir quoi !
Doraki a écrit:T'as un lien vers le sujet ?
Le site de l'UPS : http://concours-maths-cpge.fr/fichiers.php
Pour "concours" tu choisis "Banque Inter-ENS", filière "MP" puis année 2004 Paris-Cachan.
Tu trouveras l'énoncé et la correction, le correcteur est M. Gonnord.
Bon courage !
Si y'a pas une raison simple pour que ||f||0 <= C * N(infini)(f), il y a effectivement un risque de grugeage.
Il a pas expliqué pourquoi ||Ta;) - somme pour p > P des ep.Tfp;) ||0 devrait tendre vers 0.
Faudrait faire une majoration explicite de ce bazar.
Bon j'aime pas tellement la théorie de Fourier :/ donc j'ai ptetre raté un truc aussi.
Il a pas expliqué pourquoi ||Ta;) - somme pour p > P des ep.Tfp;) ||0 devrait tendre vers 0.
Faudrait faire une majoration explicite de ce bazar.
Bon j'aime pas tellement la théorie de Fourier :/ donc j'ai ptetre raté un truc aussi.
Doraki a écrit:Si y'a pas une raison simple pour que ||f||0 P des ep.Tfp;) ||0 devrait tendre vers 0.
Faudrait faire une majoration explicite de ce bazar.
Bon j'aime pas tellement la théorie de Fourier :/ donc j'ai ptetre raté un truc aussi.
En fait pour s=0 on peut faire la majoration dont tu parles (bien que le correcteur n'en dise pas un mot...). Pour s>1/2 on peut montrer que l'espace est complet et que la limite est Ta_phi (égalité des coeff de Fourrier), donc là encore ça passe.
Pour 0<s<=1/2 en revanche je ne vois pas, et de toute façon je ne pense pas que ceux qui ont élaboré le sujet attendaient ce genre de réponse... Je pense que je vais aller demander à l'école normale parce que franchement j'en dors plus la nuit !
Merci en tout cas d'avoir essayé.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
