Flux

[Nic]

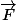
Donc voilà, il faut calculer le flux du champ vectoriel (5x³, 5y³, 5z³) au travers de la sphère d'équation x²+y²+z² 4.

Le rayon vaut donc 2. Avec les équations paramétriques, en considérant, l'angle celui qui part de l'axe Oz jusqu'au point P de la sphère et celui avec l'axe Ox... L'angle alpha est le phi du dessin et le phi le teta du dessin... dur dur ^^

http://www.uel.education.fr/consultation/reference/physique/meca/apprendre/chapitre0/01/im01/image116.gif

Comment afficher cette image sur ce forum :s...



On a:



Il faut maintenant remplacer x,y,z dans le champ vectoriel. Ensuite, il faut calculer un vecteur normal :


Une fois effectué il faut faire : et l'intégrer sur la surface. Les paramètres sont et . Si je me suis trompé dites-le moi. Par contre pour résoudre ces intégrales hmhm... J'ai besoin d'un peu d'aide. Si qqn savait le faire et me montrer comment il faut faire .

Merci :we:

[El_Gato]

Je ne comprends pas l'expression de ton vecteur normal: dans le cas d'une sphère la normale est donnée simplement par le rayon vecteur, donc ici un vecteur normal pointant vers l'extérieur est simplement:
.

Quant à l'intégrale finale elle n'est pas dure: c'est juste une intégrale double avec des bornes variant entre , pour la latitude, et 0, pour la longitude. C'est juste du calcul ennuyeux mais pas trop méchant.

[Nic]

Merci de ta réponse

hmmmm en fait c'est parce que on doit le calculer en faisant le produit vectoriel de :

vectoriellement par


Ici, u et v sont les angles et

En faisant cela j'arrive à un vecteur assez complexe. Par contre, on sait mettre sin et r en évidence. Là on se ramène à une expression à peu près comme la tienne et beaucoup plus simple. Est-ce que je peux mettre comme ça en évidence dans le vecteur normal pour le simplifier... sans pour autant changer la réponse de l'intégrale?

Sinon, ce n'est pas les bornes qui me posent problèmes mais merci quand même

Je pense que ta solution est sans doute la bonne, mais comment fais-tu pour arriver à cette expression du vecteur normal ?

[El_Gato]

Je pense que ta solution est sans doute la bonne, mais comment fais-tu pour arriver à cette expression du vecteur normal ?

Si tu prends une sphère centrée en l'origine, la normale extérieure est donnée par le rayon vecteur...

Visiblement tu as voulu recalculer la normale en prenant le produit vectoriel de deux vecteurs tangents. Ce qui est tout à fait exact, mais dans le cas de la sphère pas la peine de se fatiguer à faire un tel calcul.

[Nic]

Oui c'est vrai mais en fait je suis obligé de le calculer à chaque fois :)... c'est comme ça l'école :we: . Si je le calcule donc, puis-je mettre en évidence le sin et le r afin d'arriver au même vecteur normal que toi? Cela ne changera-t-il pas le résulat final?

:we:

[El_Gato]

Le vecteur position est .

Un vecteur normal est donc donné par le produit vectoriel:



qui est égal à c'est à dire i.e. fois le vecteur position. Sa norme au carré est .

En calculant le vecteur unitaire associé, on retrouve donc exactement le vecteur .

[Nic]

Oki j'ai compris d'où vient mon erreure, je ne calculais pas le vecteur normal unitaire mais simplement le normal ! Merci à toi !