Fonction cercle , problème (1°S)

[black bear]

Bonjour alors voici l'énoncé de l’exercice :
On considère un plan muni d'un repère orthonormé ( O ; i ; j ), la droite d'équation 3x+4y-12= 0 et le cercle (C) de centre O et de rayon 2
Partie A : Recherche de l'équation du cercle de centre A(xa;ya) et de rayon R.
1) Si M(x;y) déterminer les coordonnés de AM
Donc la rien de dur j'applique mon cours : AM(x-xa)
(y-ya)
2)Quelle est la condition caractéristique d’appartenance du point M au cercle ?
La aussi j'y arrive , Pour que M appartienne au cercle il faut que AM = R

3)Déduire des 2 questions précédentes la relation entre AM² et R²
Ils sont égaux si AM = R

4)Application : Quelle est l'équation du Cercle (C) ?
Alors la je me dit qu'il faut que la distance du A a M soit égale à 2 ( R = 2)
J'ai cherché sur internet et j'ai trouvé que la formule pour la distance entre deux point d'un repère =
V= racine
AM=V((x-xa)²+(y-ya²)) qui doit donc être = à 2

Et mon prof de math étant donné que ces collègue lui ont dit qu'il était fou de nous donner un DM aussi dur nous a donné un coup de pouce et a noté au tableau : AM²= (x-xa)²-(y-ya)²=R²
Mais pourquoi tout mettre au carré ? c'est la que je sèche et que je ne comprend pas....
Un petit peu d'aide pour comprendre ne serait pas de refus

[Manny06]

Bonjour alors voici l'énoncé de l’exercice :
On considère un plan muni d'un repère orthonormé ( O ; i ; j ), la droite d'équation 3x+4y-12= 0 et le cercle (C) de centre O et de rayon 2
Partie A : Recherche de l'équation du cercle de centre A(xa;ya) et de rayon R.
1) Si M(x;y) déterminer les coordonnés de AM
Donc la rien de dur j'applique mon cours : AM(x-xa)
(y-ya)
2)Quelle est la condition caractéristique d’appartenance du point M au cercle ?
La aussi j'y arrive , Pour que M appartienne au cercle il faut que AM = R

3)Déduire des 2 questions précédentes la relation entre AM² et R²
Ils sont égaux si AM = R

4)Application : Quelle est l'équation du Cercle (C) ?
Alors la je me dit qu'il faut que la distance du A a M soit égale à 2 ( R = 2)
J'ai cherché sur internet et j'ai trouvé que la formule pour la distance entre deux point d'un repère =
V= racine
AM=V((x-xa)²+(y-ya²)) qui doit donc être = à 2

Et mon prof de math étant donné que ces collègue lui ont dit qu'il était fou de nous donner un DM aussi dur nous a donné un coup de pouce et a noté au tableau : AM²= (x-xa)²-(y-ya)²=R²
Mais pourquoi tout mettre au carré ? c'est la que je sèche et que je ne comprend pas....
Un petit peu d'aide pour comprendre ne serait pas de refus

attention il y a une erreur de signe au tableau
si AM=V((x-xa)²+(y-ya)²)=R alors AM²=(x-xa)²+(y-ya)²=R²

[black bear]

attention il y a une erreur de signe au tableau
si AM=V((x-xa)²+(y-ya)²)=R alors AM²=(x-xa)²+(y-ya)²=R²

C'est pas si AM²=(x-xa)²+(y-ya)²=R² Alors AM= + ou - V((x-xa)²+(y-ya)²) ?

[Manny06]

C'est pas si AM²=(x-xa)²+(y-ya)²=R² Alors AM= + ou - V((x-xa)²+(y-ya)²) ?

AM est une distance donc toujours positive

[black bear]

AM est une distance donc toujours positive

Pourquoi vous ne me lancez pas sur des pistes , ce DM est au dessus du niveau de 1ère S a part les forum et mon cahier de math je n'ai aucune aide ...arrètez les réponses abstraites et proposez des vraies choses ......

[black bear]

Pourquoi vous ne me lancez pas sur des pistes , ce DM est au dessus du niveau de 1ère S a part les forum et mon cahier de math je n'ai aucune aide ...arrètez les réponses abstraites et proposez des vraies choses ......

Enfin vous ne me donnez pas des réponses abstraites mais elles ne font rien avancer , et encore je trouve que ce forum est le moin pire pour ça ....

[capitaine nuggets]

Salut !

Pourquoi vous ne me lancez pas sur des pistes , ce DM est au dessus du niveau de 1ère S a part les forum et mon cahier de math je n'ai aucune aide ...arrètez les réponses abstraites et proposez des vraies choses ......

Pour quelqu'un qui demande de l'aide, tu est bien impoli.
Pour ma part, je ne suis pas du tout convaincu que ce DM soit au-dessus du niveau de la 1re S, mais bon bref.
Par contre, le coup de "arrêtez les réponses abstraites" m'a bien fait rire :
- ta formule recopiée au tableau est incorrect parce que tu as dû mal la recopier.
L’inattention, ca arrive, ca n'est pas grave. Mais de là à chambrer Manny06 qui essaie de t'aider...
(Si tu veux faire l'exercice correctement, encore faut-il avoir les bonnes formules :++:).
- Enfin, je ne vois pas en quoi le fait de te dire que AM est une distance, elle est donc positive, peut paraître "abstrait". De toute évidence, tu n'as pas l'air de connaître la signification du mot "abstrait".
Je terminerai là-dessus en disant que ce n'est pas en étant désagréable que tu obtiendras de l'aide.

Bref, voici quelques indications :
2°) Comme ce n'est pas précisé dans la question :
Si appartient au cercle de centre et de rayon alors la condition est
3°) Il n'y a pas de "si",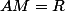 donc en élevant au carré les deux membres de l'égalité, .
4°)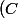 est le cercle de centre et de rayon donc n'intervient pas.
Ici, il faudra te servir de la relation obtenue d'après le théorème de Pythagore : :+++: