2 petits problèmes de proba (variable aleatoire)
15 messages
- Page 1 sur 1
2 petits problèmes de proba (variable aleatoire)
Bonjour,
j'ai 2 petits problèmes de proba pour lesquels j'ai qques soucis, en fait je n'arrive pas à bien formaliser les énoncés
il faut clquer sur le lien pour afficher l'énoncé
dans le 1er (http://img85.imageshack.us/my.php?image=1bo9.jpg) :
X suit une loi uniforme ( sur (0,1) ? ) mais ensuite je n'arrive pas à trouver les lois de N et donc de T ....
j'ai pensé à des lois geométriques mais bof ...!
J'ai surtout besoin des 3 premieres questions
dans le 2e (http://img152.imageshack.us/my.php?image=2xf7.jpg) :
question 3 : j'imagine que c'est T = X-Y mais est-ce en valeur absolue, si oui comment calculer la densité de cette loi
question 4 : je ne trouve pas la loi de Delta ... j'ai pensé à une loi geométrique mais bof ...!
Voilà ! Merci de m'aider ! Car je cherche depuis longtemps déjà ... je sais que c'est pas dur mais je trouve pas ... arrggghh !
Merci
j'ai 2 petits problèmes de proba pour lesquels j'ai qques soucis, en fait je n'arrive pas à bien formaliser les énoncés
il faut clquer sur le lien pour afficher l'énoncé
dans le 1er (http://img85.imageshack.us/my.php?image=1bo9.jpg) :
X suit une loi uniforme ( sur (0,1) ? ) mais ensuite je n'arrive pas à trouver les lois de N et donc de T ....
j'ai pensé à des lois geométriques mais bof ...!
J'ai surtout besoin des 3 premieres questions
dans le 2e (http://img152.imageshack.us/my.php?image=2xf7.jpg) :
question 3 : j'imagine que c'est T = X-Y mais est-ce en valeur absolue, si oui comment calculer la densité de cette loi
question 4 : je ne trouve pas la loi de Delta ... j'ai pensé à une loi geométrique mais bof ...!
Voilà ! Merci de m'aider ! Car je cherche depuis longtemps déjà ... je sais que c'est pas dur mais je trouve pas ... arrggghh !
Merci
D'abord, par simple curiosité, à quel niveau d'étude a-t-on ces exercices ? Sinon, voici quelques indications :
Pour le premier exercice :
1. Les suivent en effet une loi uniforme mais pas sur [0,1]. Essaye de trouver les valeurs prises par la variable
suivent en effet une loi uniforme mais pas sur [0,1]. Essaye de trouver les valeurs prises par la variable 
2. Pour les cela ressemble à des temps d'attente d'où des lois géométriques.
cela ressemble à des temps d'attente d'où des lois géométriques.
Pour le deuxième
3. On a bien car le temps d'attente est positif. Mais il faut faire attention que ici les lois sont discretes (comme dans l'autre exercice d'ailleurs) donc pas de densité.
car le temps d'attente est positif. Mais il faut faire attention que ici les lois sont discretes (comme dans l'autre exercice d'ailleurs) donc pas de densité.
Pour le premier exercice :
1. Les
2. Pour les
Pour le deuxième
3. On a bien
Merci Yipee j'ai quasiment fini ces 2 exercices !
Désolé de t'embeter encore mais j'ai encore quelques questions !
Sur les liens suivants tu peux trouver l'énoncé en noir et mes réponses en bleu ...Peux tu m'aider car je tourne en rond !
page 1 : http://img78.imageshack.us/my.php?image=11qd9.jpg
page 2 : http://img78.imageshack.us/my.php?image=12sw0.jpg
Merci Beaucoup !
Désolé de t'embeter encore mais j'ai encore quelques questions !
Sur les liens suivants tu peux trouver l'énoncé en noir et mes réponses en bleu ...Peux tu m'aider car je tourne en rond !
page 1 : http://img78.imageshack.us/my.php?image=11qd9.jpg
page 2 : http://img78.imageshack.us/my.php?image=12sw0.jpg
Merci Beaucoup !
Pour la 2. voici d'abord l'explication "avec les mains". On découpe l'espace selon les valeurs de X. C'est à dire que l'on dit que l'événement  est l'union des événements
est l'union des événements  où x décrit l'ensemble des réels. Maintenant, comme dx est un "infiniment petit" on a que A_x est "presque" l'événement
où x décrit l'ensemble des réels. Maintenant, comme dx est un "infiniment petit" on a que A_x est "presque" l'événement  dont la probabilités est
dont la probabilités est f(x)dx) car X et Y sont indépendants. Il ne reste plus qu'a faire la somme.
car X et Y sont indépendants. Il ne reste plus qu'a faire la somme.
De manière plus propre on a
 = \int_D f(x)g(y)dx dy)
où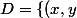 \in R^2~|~ y\leq x\}) . Il ne reste plus qu'a calculer par Fubbini.
. Il ne reste plus qu'a calculer par Fubbini.
De manière plus propre on a
où
Yipee a écrit:D'abord, par simple curiosité, à quel niveau d'étude a-t-on ces exercices ? Sinon, voici quelques indications :
Pour le premier exercice :
1. Lessuivent en effet une loi uniforme mais pas sur [0,1]. Essaye de trouver les valeurs prises par la variable
2. Pour lescela ressemble à des temps d'attente d'où des lois géométriques.
Pour la question 2., je ne pense pas que l'on puisse utiliser une loi géométrique. En effet, pour ce type de loi, les répétitions doivent être indépendantes.
D'ailleurs, pour la loi géométrique, P(X=k)=p(1-p)^(k-1)
Dans notre cas, comment calculer la probabilité de succès p, sachant que celle ci dépend du nombre de carte déjà possédées ?
Ici, même si cela n'est pas indiqué, les choix des cartes sont indépendants : on peut imaginer que comme le nombre d'images dans toutes les boites est nettement supérieur à celui des images que l'enfant va avoir, le fait d'avoir obtenu la carte numérotée 1 n'influe pas sur la probabilité de l'obtenir de nouveau.
Maintenant pour on suppose que l'enfant a déjà k-1 images différentes. Quand il en tire une il a alors une probabilité
on suppose que l'enfant a déjà k-1 images différentes. Quand il en tire une il a alors une probabilité
 d'obtenir une image qu'il n'a pas. D'où
d'obtenir une image qu'il n'a pas. D'où
 suit la loi
suit la loi )
Maintenant pour
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
