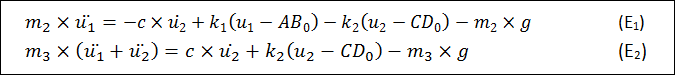leplubodeslapin a écrit:Bonsoir,
Merci pour la réponse déjà, c'est vers une histoire de matrice qu'il faut que je m'oriente je pense aussi. En fait j'ai retrouvé un TD de physique du solide où on utilisait les matrices, je te montre la méthode que l'on employait :
On posait une matrice [X] = [u1" , u2"] (en colonne) et on écrivait le système sous cette forme :
[A][X]=[B] où [A] contient les composantes en degré 2 et [B] contient ce qui reste (les u', les u et les restes). [A] est une matrice 2*2 et [B] une matrice colonne à 2 lignes.
On multipliait à gauche par l'inverse de A que je noterai "[A]-1" :
[A]-1[A][X] = [A]-1[B]
Et donc [X] = [A]-1[B] qu'on proposait de résoudre avec un logiciel, mais on est pas allé plus loin.
J'ai une licence de 2 mois pour Maple 16, j'imagine que je peux résoudre ça avec.
J'ai un peu l'impression que c'est une technique différente de la tienne mais au final assez proche. Après je ne sais pas ce qu'est cette notion d'exponentielle de matrice. Et pour diagonaliser la matrice c'est sûr ça va pas être la joie ahah, après c'est de la physique y aura assez peu d'étude de cas (en général les valeurs sont toujours positives je veux dire).
J'ai les valeurs des masses m2 et m3, les constantes c, k1 et k2 mais j'ai pas AB0 et CD0 que j'aimerai pouvoir modifier facilement pour dimensionner ma suspension.
Du coup, tu me conseilles de partir plutôt sur ta méthode ou celle que j'avais vue en TD ? (Je travaille sur un sujet bien différent de la matière où j'ai vu ce TD, c'est un travail personnel non-guidé c'est à moi de choisir les outils que je veux)
Je n'ai pas compris la méthode que tu avais déjà utilisé donc je ne peux pas vraiment t'orienter entre les deux.. En tout cas au sujet de l'exponentielle de matrice, elle est définie par la Meme série entière que pour des réels, mais avec une matrice. Et les deux grandes propriétés sont que si P est une matrice de passage, tu as
=Pexp(A)P^{-1})
et si D est une matrice diagonale alors exp(D) est une matrice diagonale avec l'exponentielle des coefficients de D. C'est pour quoi si tu peux diagonaliser ta matrice M, le calcul de l'exponentiel se fait très bien Grace à ces deux propriétés.
pour plus d'informations sur l'exponentielle de matrice et les systèmes linéaires d'equations différentiels :
[url]http://fr.m.wikiversity.org/wiki/Équation_différentielle_linéaire/Généralisation,_notation_matricielle[/url]
(ce n'est pas exactement le Meme cas toi tu as deux fonctions distinctes mais Ca doit pouvoir s'adapter).
Comme apparemment tu peux utiliser malta, il pourrait faire la diagonalisation pour toi.
Étant donné que je n'ai pas testé moi Meme cette solution dans ton cas à deu fonctions, je ne garantis pas que c'est la meilleure chose à faire et j'espère ne pas t'aiguiller sur une fausse piste.
Damien